Copula建模：从二维，多维到高维

1 概述

在许多金融应用中，我们需要对\(d\)维随机向量\(\mathbf X=(X_1,\cdots,X_d)^T\)的联合分布函数 \[ F(x_1,\cdots,x_d) = \mathbb P\left(X_1\le x_1, \cdots, X_p \le x_d \right) \tag{1}\] 建模。当随机向量\(\mathbf X\)连续时，其联合概率密度函数写作 \[ f(x_1,\cdots,x_d) = \frac{\partial^d }{\partial x_1\cdots \partial x_d}F(x_1,\cdots,x_d). \tag{2}\] 联合分布（密度）函数完整刻画了随机向量不确定规律，可提供远比协方差矩阵更全面更丰富的信息。联合分布不仅包含每个变量的边缘分布信息，还能够完整描述随机变量之间的所有关系，包括线性、非线性、高阶依赖等，因此联合分布可以捕捉极端事件下的变量关系，这在风险管理中尤为重要。

以担保债务凭证（Collateralized Debt Obligation, CDO）定价为例。CDO是一种结构性金融产品，其本质是将基础资产池的信用风险进行分级重组后发行的证券。CDO汇集公司贷款、住房抵押贷款、ABS债券、高收益债券等等生息资产形成标的资产池，然后将资产池现金流切割成不同风险等级的证券（Tranche），通过优先级/次级结构实现风险再分配。一般来说，CDO的资产池通常包含100-300个来自于不同债务人的信用风险资产，规模往往在5亿至50亿美元间。理论上，CDO产品的价格应为其资产池在未来时期预期现金流的贴现值，而CDO在各时期的现金流等于各信用风险资产未发生违约时的利息收入减去因违约而产生的损失。通常，利息收入的计算较为直接，对违约损失建模则较为复杂。假设CDO资产池包含\(d\)个信用资产，违约损失可表示为： \[ L(t) = \sum_{i=1}^p P_i(1-R_i)D_i(t) \] 其中\(D_i(t)=I(X_i \le t)\)为第\(i\)个资产在时间\(t\)是否违约的二值变量，\(X_i\)是违约时间，\(P_i\)为预期未违约本金，\(R_i\)代表违约后的回收率。在一个简单定价模型中，我们假设各资产的本金和回收率固定且已知，那么建模的核心在于准确估算违约时间向量\(\mathbf X=(X_1,\cdots,X_d)^T\)的联合分布函数。

在经典统计学框架下，多元分布建模常采用多元正态分布或多元t分布等方法，但是这类方法有很大的局限性，灵活度存在明显不足：边缘同质化限制，即要求所有边缘分布同属于特定分布族（如正态分布）；对称相关性假设，变量间依赖结构呈现椭圆对称性，无法刻画非对称尾部依赖。而且，可用于多元分布建模的分布类型也十分有限。

Copula方法通过Sklar定理实现了多元分布建模的革命性突破，该定理将 式 1 中的联合分布函数表示为 \[ F(x_1,...,x_d) = C(F_1(x_1),...,F_d(x_d)) \tag{3}\] 其中\(F_i(x_i)\)为变量\(X_i\)的边缘分布函数，函数\(C:[0,1]^d \to \mathbb R\)称为copula，它完整地刻画了变量间的依赖结构。Sklar定理表明，联合分布建模可以解耦为两个独立的步骤：1）对各变量的边缘分布建模，边缘分布属于一维分布，可供使用的分布类型较为丰富，甚至可以使用非参数估计；2）对变量间的依赖结构，也就是copula建模。例如在金融风险管理中，资产收益率可用偏态t分布描述厚尾和非对称特征，同时用clayton copula刻画危机时期的下尾部依赖特征，这样大大增加了建模的灵活性。

Copula本身是一种特殊的多元概率分布函数。考虑对所有变量\(i=1,\cdots,d\)进行概率积分变换\(U_i=F_i(X_i)\)，那么 式 3 中的copula函数\(C\)就是随机向量\(\mathbf U = (U_1,\cdots,U_d)^T\)的联合分布函数。由于概率积分变换后的变量\(U_i\)服从均匀分布，所以copula是一类定义在\([0,1]^d\)上的联合概率分布函数，其边缘分布为均匀分布，对应的copula密度函数可以定义为 \[ c(u_1,\cdots,u_d) = \frac{\partial^d }{\partial u_1\cdots \partial u_d}C(u_1,\cdots,u_d). \tag{4}\] 为了方便区分，一般习惯用大写字母\(C\)表示copula（分布）函数，用小写字母\(c\)表示copula密度函数。进一步对 式 3 等式两边依次对各分量求偏导数，可以将 式 2 中的联合概率密度函数\(f\)解耦为copula密度函数与边缘密度函数的乘积： \[ f(x_1,\cdots,x_d) = c(F_1(x_1),\cdots,F_d(x_d))\prod_{i=1}^d f_i(x_i), \tag{5}\] 其中\(f_i\)是边缘分布\(F_i\)对应的密度函数。

2 二维copula建模

我们首先介绍常用的二维copula。为了符号更加清晰，我们在本小节记二维随机向量为\((X,Y)\)，其联合分布函数和联合密度函数分别记作\(F\)和\(f\)，对应的边缘分布函数为\(F_X\)（\(F_Y\)），边缘密度函数为\(f_X\)（\(f_Y\)）。概率积分变换后的向量表示为\((U=F_X(X),V=F_Y(Y))\)，其联合分布函数\(C\)就是copula函数，相应的copula密度函数是\(c\)。

2.1 椭圆族Copula

椭圆族copula本质上是在利用已有的联合分布函数中隐含的依赖结构。由 式 3 可知\(F(x,y) = C(F_X(x),F_Y(Y))\)，那么经变换\(u=F_X(x)\)和\(v=F_Y(y)\)后可得 \[ C(u,v) = F(F_X^{-1}(u),F_Y^{-1}(v)), \tag{6}\] 其中\(F_X^{-1}\)和\(F_Y^{-1}\)分别为变量\(X\)和\(Y\)的分位数函数。Copula密度函数可以表示为 \[ c(u,v) = \frac{f(F_X^{-1}(u),F_Y^{-1}(v))}{f_X(F_X^{-1}(u))f_Y(F_Y^{-1}(v))}. \tag{7}\] 当\(F\)为已知的联合分布函数时，我们可以使用 式 6 或者 式 7 抽取\(F\)中隐含的copula来进行建模。

高斯Copula。 当\(F=\Phi_{\rho}\)为相关系数\(\rho\)的标准二元正态分布函数时，所构造出的copula称为高斯copula，它的表达式写作 \[ C_{\rho}^{Ga}(u,v) = \Phi_{\rho}(\Phi^{-1}(u), \Phi^{-1}(v)), \] 其中\(\Phi^{-1}\)表示标准正态分布的分位数函数，高斯copula密度函数是 \[ c_{\rho}^{Ga}(u,v) = \frac{1}{\sqrt{1-\rho^2}} \exp\left(-\frac{\rho^2(x^2 + y^2) - 2\rho xy}{2(1-\rho^2)}\right) \] 其中\(x = \Phi^{-1}(u)\), \(y = \Phi^{-1}(v)\)。高斯copula包含一个参数\(\rho \in (-1, 1)\)。

Student t Copula。 当\(F=t_{\rho,\nu}\)为自由度为\(\nu\)相关系数为\(\rho\)的二元t分布函数，所构造出的copula称为t copula，它的表达式写作 \[ C_{\rho,\nu}^{t}(u,v) = t_{\rho,\nu}(t_{\nu}^{-1}(u), t_{\nu}^{-1}(v)) \] 其中\(t_{\nu}^{-1}\)为自由度为\(\nu\)的t分布的分位数函数。相应的copula密度函数是 \[ c_{\rho,\nu}^{t}(u,v) = \frac{\Gamma(\frac{\nu+2}{2})\Gamma(\frac{\nu}{2})}{\Gamma(\frac{\nu+1}{2})^2} \frac{1}{\sqrt{1-\rho^2}} \left(1+\frac{x^2+y^2-2\rho xy}{\nu(1-\rho^2)}\right)^{-\frac{\nu+2}{2}}, \] 其中参数取值范围为\(\rho \in (-1, 1)\), \(\nu > 2\)。

library(copula)
library(lattice)
library(colorspace)

## 参数设置
rho <- 0.7  # 相关系数
nu <- 3     # t copula自由度
grid_points <- 50  # 网格密度

## 生成网格数据
u <- seq(0.01, 0.99, length.out = grid_points)  # 避免边界问题
grid <- expand.grid(u = u, v = u)

## 计算copula密度
# Gaussian copula
norm_cop <- normalCopula(param = rho, dim = 2)
grid$d_norm <- dCopula(as.matrix(grid[,c('u','v')]), norm_cop)

# t copula
t_cop <- tCopula(param = rho, dim = 2, df = nu)
grid$d_t <- dCopula(as.matrix(grid[,c('u','v')]), t_cop)

## 3D图形绘制
par(mfrow = c(1, 2), mar = c(1, 1, 2, 1))

# Gaussian copula密度图
persp(matrix(grid$d_norm, nrow = grid_points), 
      theta = -30, phi = 20, col = hcl.colors(50, "Blues"), 
      xlab = "u", ylab = "v", zlab = "密度",
      main = paste0("Gaussian Copula\n(ρ=", rho, ")"),
      border = NA, shade = 0.5, ticktype = "detailed")

# t copula密度图
persp(matrix(grid$d_t, nrow = grid_points),
      theta = -30, phi = 20, col = hcl.colors(50, "Reds"),
      xlab = "u", ylab = "v", zlab = "密度", 
      main = paste0("t-Copula\n(ρ=", rho, ", ν=", nu, ")"),
      border = NA, shade = 0.5, ticktype = "detailed")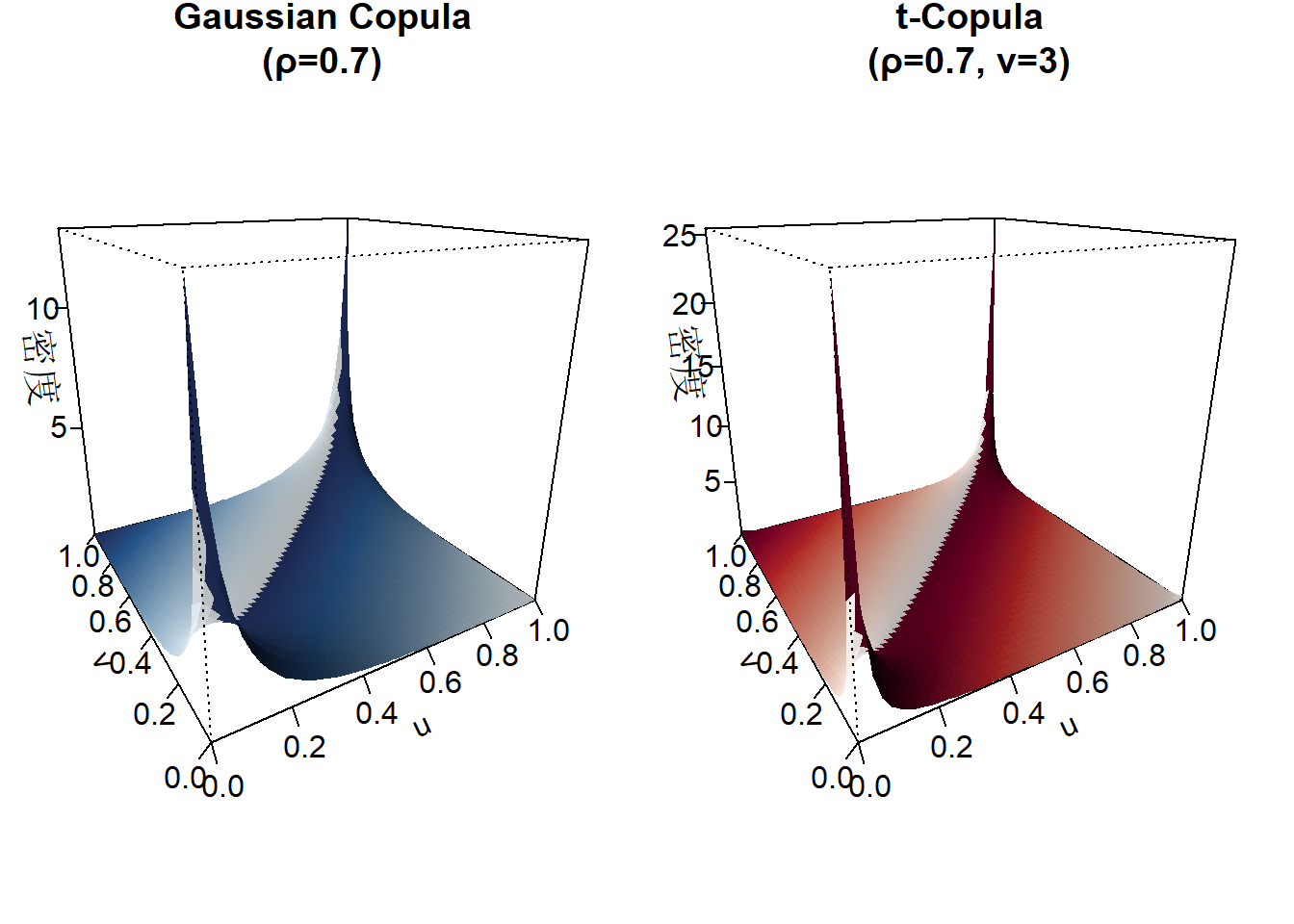

2.2 阿基米德族Copula

阿基米德Copula是一类通过生成元（Generator）函数构造的Copula，生成元在构建Copula的过程中起到了核心作用。生成元\(\phi:[0,1] \to [0,\infty]\)是连续且严格递减的凸函数，满足\(\psi(1)=0\)以及\(\psi(0)\le \infty\)。

通过生成元构建阿基米德Copula的核心公式是 \[ C(u,v) = \psi^{[-1]}(\psi(u) + \psi(v)) \tag{8}\] 其中\(\psi^{[-1]}\)为生成元的伪逆函数： \[ \psi^{[-1]}(t) = \begin{cases} \psi^{-1}(t), & 0 \leq t \leq \psi(0) \\\ 0, & t > \psi(0). \end{cases} \] 当\(\psi(0)=\infty\)时，伪逆函数就是生成元的逆函数。可以证明， 式 8 满足copula函数所需要的边界条件\(C(u,0)=C(0,v)=0\)，\(C(u,1)=u\)以及\(C(1,v)=v\)。

通过变换生成元的形式可以生成多种类型的阿基米德copula，我们在 表 1 中列出了几种常用的类型。

表 1: 常用的阿基米德copula

类型	生成元与参数	Copula函数与密度
Clayton	\(\psi(t)=\frac{1}{\theta}(t^{-\theta}-1)\) \(\theta > 0\)	C(u,v): \(\left(u^{-\theta} + v^{-\theta}-1\right)^{-1/\theta}\) c(u,v): \(\frac{(1+\theta)(uv)^{-\theta-1}}{(u^{-\theta}+v^{-\theta}-1)^{\frac{\theta+2}{\theta}}}\)
Gumbel	\(\psi(t)=(-\ln t)^{\theta}\) \(\theta \geq 1\)	C(u,v): \(\exp\left(-\left[(-\ln u)^{\theta}+(-\ln v)^{\theta}\right]^{1/\theta}\right)\) c(u,v): \(\frac{C(u,v)(\ln u \ln v)^{\theta-1}}{uv\left[(-\ln u)^{\theta} + (-\ln v)^{\theta}\right]^{2-1/\theta}}\left(1+\frac{\theta-1}{\left[(-\ln u)^{\theta} + (-\ln v)^{\theta}\right]^{1/\theta}}\right)\)
Frank	\(\psi(t)=-\ln\frac{e^{-\theta t}-1}{e^{-\theta}-1}\) \(\theta \neq 0\)	C(u,v): \(-\frac{1}{\theta}\ln\left(1+\frac{(e^{-\theta u}-1)(e^{-\theta v}-1)}{e^{-\theta}-1}\right)\) c(u,v): \(\frac{\theta(1-e^{-\theta})e^{-\theta(u+v)}}{\left[(1-e^{-\theta})-(1-e^{-\theta u})(1-e^{-\theta v})\right]^2}\)
Joe	\(\psi(t)=-\ln\left(1-(1-t)^{\theta}\right)\) \(\theta \geq 1\)	C(u,v): \(1-\left[(1-u)^{\theta}+(1-v)^{\theta}-(1-u)^{\theta}(1-v)^{\theta}\right]^{1/\theta}\) c(u,v): \(\frac{(1-u)^{\theta-1}(1-v)^{\theta-1}[\theta-1+(1-u)^{\theta}+(1-v)^{\theta}]}{\left[(1-u)^{\theta}+(1-v)^{\theta}-(1-u)^{\theta}(1-v)^{\theta}\right]^{2-1/\theta}}\)

这4种常用的阿基米德copula都只包含一个参数，该参数决定了依赖关系的强度。 Clayton：参数\(\theta\)控制下尾依赖强度，\(\theta \to 0\)时退化为独立copula。Gumbel：参数\(\theta\)控制上尾依赖强度，\(\theta=1\)时退化为独立copula。Frank：唯一具有径向对称性的阿基米德copula，\(\theta>0\)时正相关，\(\theta<0\)时负相关。Joe：与Gumbel类似但生成元结构不同。

library(plotly)
library(copula)

## 增强参数设置
copula_config <- list(
  Gaussian = list(rho = 0.7, color = "Blues"),
  t = list(rho = 0.7, nu = 3, color = "Reds"),
  Clayton = list(theta = 3, color = "Greens"),
  Gumbel = list(theta = 2, color = "Purples"),
  Frank = list(theta = 8, color = "Oranges"),
  Joe = list(theta = 2, color = "Greys")
)

## 生成高精度网格
grid_res <- 200
u <- seq(0.01, 0.99, length.out = grid_res)
grid <- expand.grid(u = u, v = u)

## 创建3D曲面图函数
create_surface <- function(cop_type) {
  # 生成copula密度
  cop <- switch(cop_type,
                Gaussian = normalCopula(copula_config$Gaussian$rho),
                t = tCopula(copula_config$t$rho, df = copula_config$t$nu),
                Clayton = claytonCopula(copula_config$Clayton$theta),
                Gumbel = gumbelCopula(copula_config$Gumbel$theta),
                Frank = frankCopula(copula_config$Frank$theta),
                Joe = joeCopula(copula_config$Joe$theta))
  
  density <- dCopula(as.matrix(grid), cop)
  
  # 转换为矩阵格式
  z <- matrix(density, nrow = grid_res)
  
  # 创建plotly图形
  plot_ly(x = u, y = u, z = z, colors = viridis::viridis(100)) %>%
    add_surface(
      contours = list(
        z = list(show=TRUE, usecolormap=TRUE, highlightcolor="#ff0000", project=list(z=TRUE))
      ),
      lighting = list(ambient = 0.95),
      colorbar = list(title = "密度")
    ) %>%
    layout(
      scene = list(
        xaxis = list(title = "u"),
        yaxis = list(title = "v"),
        zaxis = list(title = "密度"),
        camera = list(eye = list(x = 1.5, y = -1.5, z = 0.8))
      ),
      title = paste(cop_type, "Copula Density")
    )
}

## 生成所有图形
create_surface("Gaussian")

create_surface("t")

create_surface("Clayton")

create_surface("Gumbel")

create_surface("Frank")

create_surface("Joe")

2.3 Copula与常用的相关性指标

Copula完整全面地描述了变量之间的依赖关系。常用的相关性指标只从某一侧面描述依赖关系，这些指标均可以由copula进行表示。

线性相关系数（Pearson相关系数）主要捕捉变量之间的线性关系。对随机变量\(X\)和\(Y\)，其线性相关系数定义为： \[ \rho = \frac{E[XY]-E[X]E[Y]}{\sqrt{Var[X]Var[Y]}}, \] 其中\(E[XY]\)可以通过概率积分变换\(U=F_X(X)\), \(V=F_Y(Y)\)表示为： \[ E[XY] = \int_0^1\int_0^1 \left[F_X^{-1}(u)F_Y^{-1}(v)\right]c(u,v)dudv. \] 需要注意的是，线性相关系数不仅仅取决于copula函数，还取决于变量的边缘分布，因此不能由copula唯一确定。

Kendall’s tau是一种非参数的秩相关系数，用于衡量两个变量之间的单调相关性。它的定义基于一致性的概念，即两个观测点是否在变量\(X\)和\(Y\)方向上具有一致的排序。假设\((\tilde X, \tilde Y)\)与\((X,Y)\)独立同分布，Kendall’s tau的原始定义是： \[ \tau = P[(X- \tilde X)(Y- \tilde Y)>0] - P[(X- \tilde X)(Y- \tilde Y)<0], \tag{9}\] 即步调一致的概率减去步调相反的概率。对于\(n\)个观测样本\((X_t,Y_t):\; t=1,\cdots,n\)，Kendall’s tau的估计量为 \[ \hat{\tau} = \frac{2}{n(n-1)} \sum_{t<t'} \text{sign}[(X_t-X_{t'})(Y_t-Y_{t'})]. \tag{10}\] 由于Kendall’s tau只取决于变量的相对排序，它不依赖于变量的边缘分布，可以由copula完全决定，表达式为 \[ \tau = 4\int_0^1\int_0^1 C(u,v)dC(u,v) - 1. \tag{11}\] 根据 式 11 ，我们可以计算常见copula的Kendall’s tau的表达式，见 表 2

表 2: 常见copula的Kendall’s tau表达式

Copula类型	参数范围	Kendall’s τ表达式
Gaussian	\(\rho \in (-1,1)\)	\(\tau = \frac{2}{\pi} \arcsin(\rho)\)
Student’s t	\(\rho \in (-1,1)\) \(\nu > 2\)	\(\tau = \frac{2}{\pi} \arcsin(\rho)\) (与自由度\(\nu\)无关)
Clayton	\(\theta > 0\)	\(\tau = \frac{\theta}{\theta + 2}\)
Frank	\(\theta \neq 0\)	\(\tau = 1 - \frac{4}{\theta}\left[1 - D_1(\theta)\right]\) 其中\(D_1(\theta) = \frac{1}{\theta} \int_0^\theta \frac{t}{e^t-1}dt\)，即Debye函数
Gumbel	\(\theta \geq 1\)	\(\tau = 1 - \frac{1}{\theta}\)
Joe	\(\theta \geq 1\)	\(\tau = 1 + \frac{4}{\theta^2}\int_0^1 u \ln u (1-u)^{2(1-\theta)/\theta}du\)

尾部依赖指数（Tail Dependence）测度变量\(X\)和\(Y\)在各自分布尾部区域的联动性，简单说，尾部依赖度量给定一个变量在尾部区域时另一个变量同样也处于相应尾部区域的概率。主要分为上尾部依赖 \[ \lambda_U = \lim_{u \to 1} P(F_X^{-1}(X) > u | F_Y^{-1}(Y) > u) \] 和下尾部依赖 \[ \lambda_L = \lim_{q \to 0} P(F_X^{-1}(X) \leq u | F_Y^{-1}(Y) < u). \] 很显然，尾部依赖指数也不依赖变量的边缘分布，只取决于变量间的依赖结构。通过简单的变量替换，上尾部依赖指数和下尾部依赖指出可以分别由copula函数表示为 \[ \lambda_U = \lim_{u \to 1}\frac{1-2u+C(u,u)}{1-u} \] 和 \[ \lambda_L = \lim_{u \to 0}\frac{C(u,u)}{u}. \] 我们在 表 3 中列出常见copula的尾部依赖指数表达式以及各自的尾部依赖特征。

表 3: 常见copula的尾部依赖指数

Copula类型	参数范围	下尾依赖指数 \(\lambda_L\)	上尾依赖指数 \(\lambda_U\)	尾部依赖特性
Gaussian	\(\rho \in (-1,1)\)	\(0\)	\(0\)	无尾依赖
Student’s t	\(\rho \in (-1,1)\) \(\nu > 2\)	\(2t_{\nu+1}\left(-\sqrt{\nu+1}\frac{\sqrt{1-\rho}}{\sqrt{1+\rho}}\right)\)	同左	对称双尾依赖
Clayton	\(\theta > 0\)	\(2^{-1/\theta}\)	\(0\)	强下尾依赖
Frank	\(\theta \neq 0\)	\(0\)	\(0\)	无尾依赖
Gumbel	\(\theta \geq 1\)	\(0\)	\(2 - 2^{1/\theta}\)	强上尾依赖
Joe	\(\theta \geq 1\)	\(0\)	\(2 - 2^{1/\theta}\)	强上尾依赖

2.4 常用copula交互式可视化

以下代码基于shiny包，请复制到本地运行。该段代码提供了常用copula可视化的工具。

library(shiny)
library(plotly)
library(copula)
library(viridis)


# 交互界面
ui <- fluidPage(
  titlePanel(""),
  sidebarLayout(
    sidebarPanel(
      selectInput("cop_type", "Copula类型:",
                  c("Gaussian", "t", "Clayton", "Gumbel", "Frank", "Joe")),
      
      # 动态参数控制
      conditionalPanel(
        condition = "input.cop_type == 'Gaussian' || input.cop_type == 't'",
        sliderInput("rho", "相关系数ρ:", 
                    min = -0.95, max = 0.95, value = 0.7, step = 0.05)
      ),
      conditionalPanel(
        condition = "input.cop_type == 't'",
        numericInput("nu", "自由度ν:", value = 4, min = 2, max = 30)
      ),
      conditionalPanel(
        condition = "input.cop_type == 'Clayton'",
        sliderInput("clayton_theta", "θ参数:", 
                    min = 0.1, max = 10, value = 3, step = 0.1)
      ),
      conditionalPanel(
        condition = "input.cop_type == 'Gumbel'",
        sliderInput("gumbel_theta", "θ参数:", 
                    min = 1.1, max = 10, value = 2, step = 0.1)
      ),
      conditionalPanel(
        condition = "input.cop_type == 'Frank'",
        sliderInput("frank_theta", "θ参数:", 
                    min = -50, max = 50, value = 8, step = 1)
      ),
      conditionalPanel(
        condition = "input.cop_type == 'Joe'",
        sliderInput("joe_theta", "θ参数:", 
                    min = 1.1, max = 10, value = 2, step = 0.1)
      ),
      
      hr(),
      sliderInput("grid_res", "网格分辨率:", 
                  min = 30, max = 100, value = 50, step = 10),
      actionButton("update", "更新视图"),
      
      # 统计量显示
      hr(),
      h4("依赖指标分析"),
      htmlOutput("kendallTau"),
      htmlOutput("tailDep"),
      HTML("<small>注：参数无效时将显示N/A</small>")
    ),
    
    mainPanel(
      plotlyOutput("copulaPlot", height = "800px")
    )
  )
)

# 服务器逻辑
server <- function(input, output) {
  # 生成网格数据
  grid_data <- reactive({
    req(input$grid_res)
    u <- seq(0.01, 0.99, length.out = input$grid_res)
    expand.grid(u = u, v = u)
  })
  
  # 当前Copula对象
  current_copula <- eventReactive(input$update, {
    type <- input$cop_type
    tryCatch(switch(type,
                    Gaussian = normalCopula(input$rho),
                    t = tCopula(input$rho, df = input$nu),
                    Clayton = claytonCopula(input$clayton_theta),
                    Gumbel = gumbelCopula(input$gumbel_theta),
                    Frank = frankCopula(input$frank_theta),
                    Joe = joeCopula(input$joe_theta)),
             error = function(e) NULL)
  })
  
  # 计算依赖指标
  calculate_measures <- reactive({
    cop <- current_copula()
    if(is.null(cop)) return(list(tau = NA, upper_tail = NA, lower_tail = NA))
    
    type <- input$cop_type
    tryCatch({
      # Kendall's tau计算
      tau_value <- if(type %in% c("Gaussian", "t")) {
        (2/pi)*asin(input$rho)
      } else {
        tau(cop)
      }
      
      # 尾部依赖计算
      tail_upper <- switch(type,
                           Clayton = 0,
                           Gumbel = 2 - 2^(1/input$gumbel_theta),
                           Joe = 2 - 2^(1/input$joe_theta),
                           t = "存在对称尾依赖",
                           0
      )
      tail_lower <- switch(type,
                           Clayton = 2^(-1/input$clayton_theta),
                           t = "存在对称尾依赖",
                           0
      )
      
      list(tau = tau_value, upper_tail = tail_upper, lower_tail = tail_lower)
    }, error = function(e) list(tau = NA, upper_tail = NA, lower_tail = NA))
  })
  
  # 渲染统计量
  output$kendallTau <- renderUI({
    measures <- calculate_measures()
    value <- if(is.na(measures$tau)) "N/A" else round(measures$tau, 3)
    HTML(paste0("<span style='color:#2c7bb6;'><b>Kendall's τ:</b> ", value, "</span>"))
  })
  
  output$tailDep <- renderUI({
    measures <- calculate_measures()
    type <- input$cop_type
    tail_text <- switch(type,
                        Gaussian = "上下尾依赖均为0",
                        t = measures$upper_tail,
                        Clayton = paste("下尾依赖:", round(measures$lower_tail,3)),
                        Gumbel = paste("上尾依赖:", round(measures$upper_tail,3)),
                        Frank = "无尾依赖",
                        Joe = paste("上尾依赖:", round(measures$upper_tail,3)),
                        "无尾依赖"
    )
    HTML(paste0("<span style='color:#d7191c;'><b>尾部依赖:</b> ", tail_text, "</span>"))
  })
  
  # 渲染3D图形
  output$copulaPlot <- renderPlotly({
    cop <- current_copula()
    validate(need(!is.null(cop), "参数组合无效，请调整参数"))
    
    grid <- grid_data()
    density <- dCopula(as.matrix(grid), cop)
    
    plot_ly(x = ~seq(0.01, 0.99, length.out = input$grid_res),
            y = ~seq(0.01, 0.99, length.out = input$grid_res),
            z = ~matrix(density, nrow = input$grid_res)) %>%
      add_surface(
        colorscale = list(seq(0, max(density), length=100), viridis(100)),
        contours = list(
          z = list(show=TRUE, project=list(z=TRUE))
        ),
        lighting = list(ambient = 0.95)
      ) %>%
      layout(
        scene = list(
          xaxis = list(title = "u"),
          yaxis = list(title = "v"),
          zaxis = list(title = "密度"),
          camera = list(eye = list(x = 1.5, y = -1.5, z = 0.8))
        ),
        title = paste(input$cop_type, "Copula 密度曲面")
      )
  })
}

# 运行应用
shinyApp(ui, server)

2.5 Copula估计与选择

2.5.1 最大似然估计

给定样本容量为\(n\)的独立同分布样本\((X_t,Y_t):\; t=1,\cdots,n\)。假定随机向量\((X,Y)\)之间的copula属于特定的参数类型\(c(\cdot,\cdot;\theta)\)，比如上面介绍的常见copula中的一种，其中\(\theta\)是该类copula中的未知参数，那么copula估计问题就转换为未知参数\(\theta\)的估计。

由于copula密度函数\(c(\cdot,\cdot;\theta)\)是随机向量\((U=F_X(X),V=F_Y(Y))\)的概率密度函数，假设边缘分布函数\(F_X\)与\(F_Y\)已知，那么我们可以将样本进行变换\(U_t = F_X(X_t)\)，\(V_t = F_Y(Y_t)\)，那么\((U_t,V_t):\; t=1,\cdots,n\)就可以视作随机向量\((U,V)\)中生成的独立同分布样本，进而可以使用最大似然法进行估计\(\hat \theta = \arg\min_\theta \sum_{t=1}^n \ln c(U_t,V_t;\theta)\)。

但是，现实中边缘分布函数\(F_X\)与\(F_Y\)通常未知，因此在copula的估计中首先要解决边缘分布函数的估计问题，一种常用的选择是使用经验分布函数，经验分布是一种非参数估计量，即无需对边缘分布的类型做进一步假设。我们总结copula估计的两个步骤：

• 定义经验分布函数 \[ \hat F_X(x) = \frac{1}{n}\sum_{t=1}^n I(X_t \le x) \quad \quad \text{和} \quad \quad \hat F_Y(y) = \frac{1}{n}\sum_{t=1}^n I(Y_t \le y). \] 进而得到变换后的样本\((\hat U_t=\hat F_X(X_t),\hat V_t=\hat F_Y(Y_i)):\; t=1,\cdots,n\)。

• 最大化对数似然函数得到估计\(\hat \theta = \arg\min_\theta \sum_{t=1}^n \ln c(\hat U_t,\hat V_t;\theta)\)。

2.5.2 逆Kendall’s tau估计

如 表 2 所示，Kendall’s tau与copula中的未知参数\(\theta\)存在一一对应关系，我们写作\(\tau = g(\theta)\)。反过来，我们可以使用逆函数\(g^{-1}\)来表示该一一对应关系：\(\theta = g^{-1}(\tau)\)。这意味着，如果我们知道变量\(X\)与\(Y\)之间的kendall’s tau，那么就可以反推出对应的参数值。

逆Kendall’s tau估计的两个步骤：1）基于样本\((X_t,Y_t):\; t=1,\cdots,n\)，通过 式 10 估计Kendall’s tau，记作\(\hat \tau\)；2）根据所假设的copula类型，确定该类型Kendall’s tau与未知参数的函数关系\(g\)以及相应的逆函数\(g^{-1}\)，进而得出估计\(\hat \theta = g^{-1}(\hat \tau)\)。

与最大似然法比较，逆Kendall’s tau估计无需估计变量的边缘分布函数，在计算上也无需数值优化，更为简便；但是，逆Kendall’s tau仅适用于估计包含一个未知参数的copula，且估计效率低于最大似然法。

2.5.3 模型选择

上述copula估计只解决了在给定copula类型的前提下如何估计其中的未知参数问题，那么应该如何选择copula类型呢？我们可以使用最小化信息准则，比如常用的AIC或者BIC，来解决这一模型选择问题。

AIC的公式写作 \[ \mathrm{AIC} = -2 \sum_{t=1}^n \ln c(\hat U_t,\hat V_t;\hat \theta) + 2 k, \] 其中\(\hat \theta\)是给定copula类型\(c(\cdot,\cdot;\theta)\)下的最大似然估计，\(k\)是该copula类型中未知参数的个数，度量了所假定copula模型的复杂度。高斯copula和常用的阿基米德copula一般包含一个未知参数，即\(k=1\)；t copula包含两个未知参数，\(k=2\)。AIC表达式的第一项度量了模型的拟合优度，第二项\(2k\)是对模型复杂度的惩罚。施加惩罚的原因是：在具有相似拟合优度的模型中间，一般来说，我们倾向于简单模型。 BIC的公式写作 \[ \mathrm{BIC} = -2 \sum_{t=1}^n \ln c(\hat U_t,\hat V_t;\hat \theta) + \ln(n) \cdot k, \] 其中\(n\)是样本容量。与AIC相比，BIC对模型复杂度的惩罚力度更强，因为一般来说\(\ln (n) > 2\)。

我们总结copula模型选择步骤如下：1）确定模型备选集，通常是常用的椭圆族copula和阿基米德copula模型，R中的VineCopula包提供了30多种copula模型可供选择；2）对于每一个copula模型，使用最大似然法估计其中的未知参数，并计算相应的AIC或者BIC值；3）选出备选集中AIC或者BIC最小的模型。

2.5.4 实际应用

估计上证综指和创业板指数日度收益率之间的copula。使用近5年的数据。

# 加载必要包
library(pedquant)    
library(quantmod)
library(tidyverse)
library(VineCopula)


# 获取上证综指和创业板数据
dat <- md_stock(
  symbol = c("000001.sh","399006.sz"), 
  date_range = "5y", 
  source = "163",    # 网易财经数据源
  adjust = "hfq"     # 后复权处理
) 

1/2 000001.sh
2/2 399006.sz

# 计算日度收益率
dat <- lapply(dat, function(df) {
  df$date <- as.Date(df$date)
  # 创建xts对象
  df <- xts(df$close_adj, order.by = df$date)
  # 计算收益率
  periodReturn(df, period = 'daily', type = "log")
})


# 按照日期合并
dat <- reduce(dat, .f = merge.xts, join = 'inner')
colnames(dat) <- c("000001.sh","399006.sz")

# 转换为矩阵格式
dat <- as.matrix(dat)


# 计算Kendall's tau
TauMatrix(dat)

          000001.sh 399006.sz
000001.sh 1.0000000 0.5611659
399006.sz 0.5611659 1.0000000

# 使用经验分布对样本进行变换
dat <- apply(dat, MARGIN = 2, FUN = function(z) rank(z)/(length(z)+1))

# 计算尾部依赖指数，u=1/sqrt(n)
u <- 1/sqrt(nrow(dat))

mean(dat[,1] <= u & dat[,2] <= u) / u # 下尾部依赖

[1] 0.4885138

2 - (1- mean(dat[,1] <= 1-u & dat[,2] <= 1-u)) / u # 上尾部依赖

[1] 0.5057224

# 拟合t copula
BiCopEst(u1 = dat[,1], u2 = dat[,2], family = 2, method = 'mle') # 最大似然法

Bivariate copula: t (par = 0.78, par2 = 5.37, tau = 0.57) 

# 在copula模型备选集中选出最优的模型
cop <- BiCopSelect(u1 = dat[,1], u2 = dat[,2], selectioncrit = 'AIC')
cop

Bivariate copula: Survival BB1 (par = 0.48, par2 = 1.85, tau = 0.57) 

# 绘制copula估计的图像
plot(cop, margins = 'unif')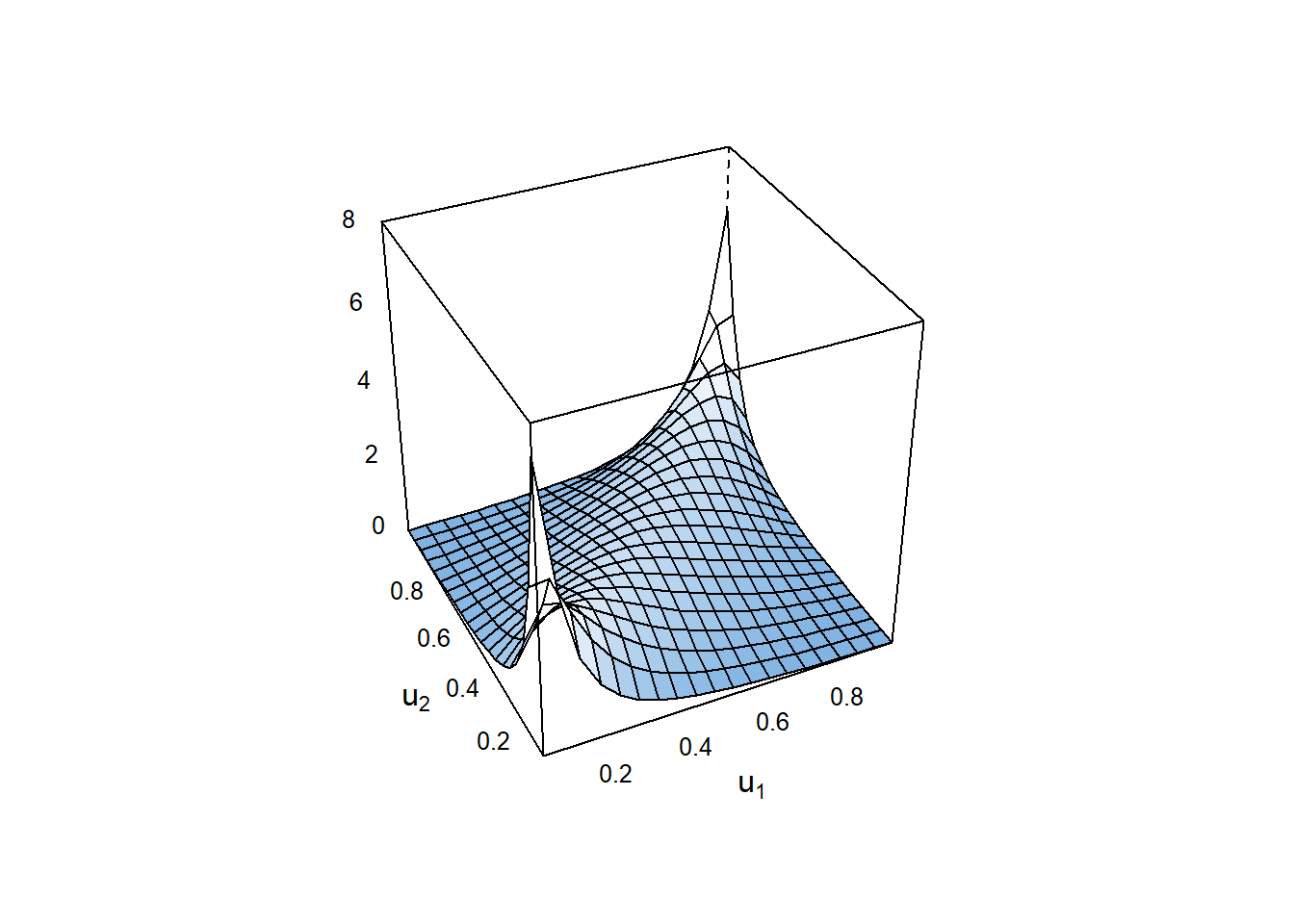

contour(cop, margins = 'unif')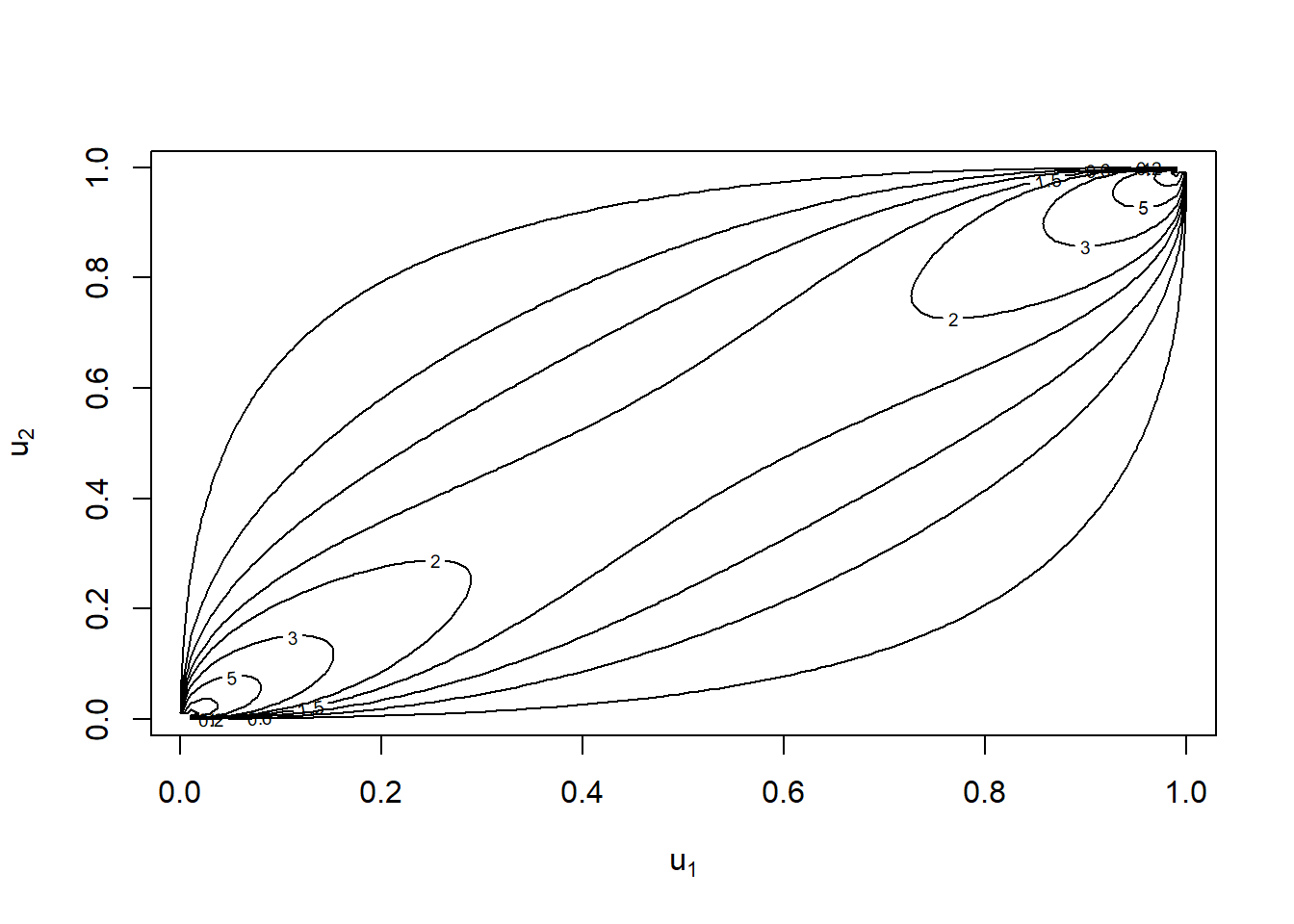

3 多维copula建模：Vine copula

本节所说的多维copula指维度\(d\ge 3\)，但一般不超过20。尽管二维copula建模有较为丰富的参数模型，但是当\(d\ge 3\)时，可选择的模型极为受限。一种选择是将椭圆族copula 式 6 或者阿基米德族copula 式 8 直接拓展到多维，但是这种方式对变量两两间的依赖结构限制过强。另一种选择是vine copula，主要思想是将二维copula模型当作“积木块”，按照一定的结构（vine）组装起来，形成多维copula，这一方式大大增加了建模的灵活性。

3.1 三维copula的分解

我们以\(d=3\)维为例，说明如何将多维copula分解按照一定结构进行分解。考虑随机向量 \(\mathbf X = (X_1,X_2,X_3)\)，记联合概率密度函数为\(f\)，边缘概率密度函数分别为\(f_1,\; f_2\)和\(f_3\)。根据条件概率公式，可以将联合密度函数分解为 \[ f(x_1,x_2,x_3) = f_{3|12}(x_3|x_1,x_2)f_{2|1}(x_2|x_1)f_1(x_1), \tag{12}\] 其中\(f_{3|12}(x_3|x_1,x_2)\)表示\(X_3\)给定\((X_1=x_1,\;X_2=x_2)\)下的条件概率密度函数，其它条件概率密度记号依此类推。

在 式 12 中，我们首先考虑条件概率密度\(f_{2|1}\)，希望将它表示成二维copula密度和边缘密度乘积的形式。我们有 \[ \begin{aligned} f_{2|1}(x_2|x_1) &= \frac{f_{12}(x_1,x_2)}{f_1(x_1)} \\ &= \frac{c_{12}(F_1(x_1),F_2(x_2))f_1(x_1)f_2(x_2)}{f_1(x_1)} \\ &= c_{12}(F_1(x_1),F_2(x_2))f_2(x_2). \end{aligned} \tag{13}\] 进一步，我们同样希望将\(f_{3|12}\)表示为二维copula密度和边缘密度的乘积形式，有 \[ \begin{aligned} f_{3|12}(x_3|x_1,x_2) &= \frac{f_{13|2}(x_1,x_3|x_2)}{f_{1|2}(x_1|x_2)} \\ &= \frac{c_{13|2}(F_{1|2}(x_1|x_2),F_{3|2}(x_3|x_2)|x_2)f_{1|2}(x_1|x_2)f_{3|2}(x_3|x_2)}{f_{1|2}(x_1|x_2)}\\ &= c_{13|2}(F_{1|2}(x_1|x_2),F_{3|2}(x_3|x_2)|x_2)f_{3|2}(x_3|x_2) \\ &= c_{13|2}(F_{1|2}(x_1|x_2),F_{3|2}(x_3|x_2)|x_2) \frac{c_{23}(F_2(x_2),F_3(x_3))f_2(x_2)f_3(x_3)}{f_2(x_2)} \\ &= c_{13|2}(F_{1|2}(x_1|x_2),F_{3|2}(x_3|x_2)|x_2)c_{23}(F_2(x_2),F_3(x_3))f_3(x_3), \end{aligned} \tag{14}\] 其中\(c_{13|2}(F_{1|2}(x_1|x_2),F_{3|2}(x_3|x_2)|x_2)\)是条件分布\((X_1,X_3)|X_2=x_2\)对应的copula密度函数。将 式 14 和 式 13 代入 式 12 中，得到 \[ f(x_1,x_2,x_3) = c_{13|2}(F_{1|2}(x_1|x_2),F_{3|2}(x_3|x_2)|x_2)c_{23}(F_2(x_2),F_3(x_3))c_{12}(F_1(x_1),F_2(x_2))f_1(x_1)f_2(x_2)f_3(x_3), \] 这意味着我们有了如下的三维copula密度分解公式： \[ c(F_1(x_1),F_2(x_2),F_3(x_3)) = c_{13|2}(F_{1|2}(x_1|x_2),F_{3|2}(x_3|x_2)|x_2)c_{23}(F_2(x_2),F_3(x_3))c_{12}(F_1(x_1),F_2(x_2)), \tag{15}\] 其中\(c_{13|2}\)，\(c_{12}\)和\(c_{23}\)都属于二维copula。

3.2 Copula分解的树表示

三维copula概率密度分解方式并不是唯一的，而是有很多可能性，一般来说对于\(d\)维变量，可能的分解方式有\(d!\times 2^{(d-2)(d-3)/2-1}\)种。每一种分解方式对应一种树结构（R-vine tree structure），以 式 15 为例，我们在 图 1 中展示了其对应的树结构。

library(VineCopula)
rvm <- RVineMatrix(Matrix = matrix(c(3,1,2,0,2,1,0,0,1),3,3))
par(mfrow = c(1,2))
plot(rvm, tree = 1)
plot(rvm, tree = 2)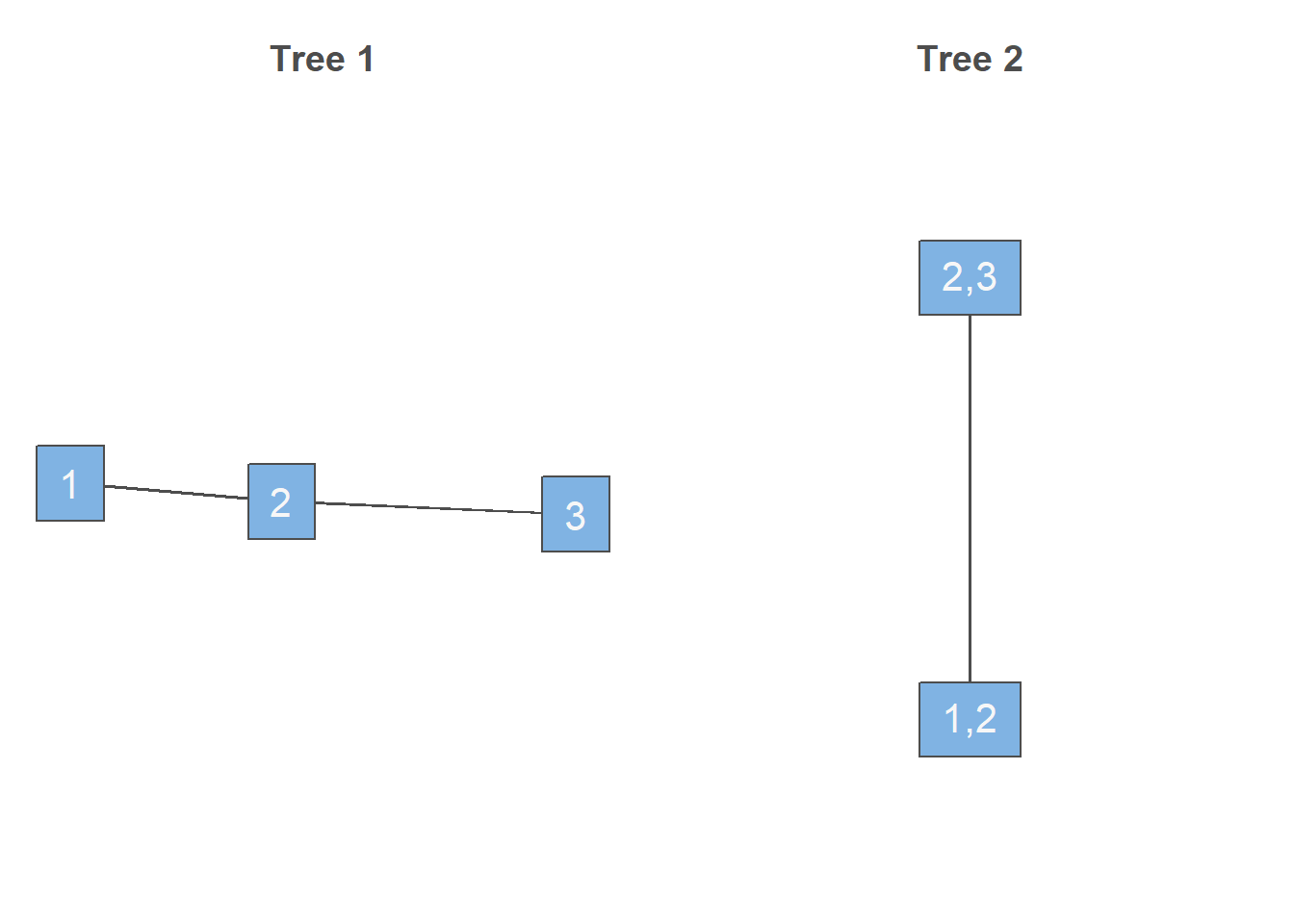

图 1: Copula分解 式 15 对应的树结构图

我们结合 图 1 介绍Copula分解的树结构。一般来说，\(d\)维变量的树结构包含\(d-1\)个有序树图，每一棵树由若干节点（node）和边线（edges）组成，其中：

• 第1棵树的节点为所有\(d\)个变量，边线指明了“边缘copula”的组合。比如变量1和2相连、变量2和3相连对应了 式 15 中的“边缘copula”\(c_{12}\)和\(c_{23}\)。

• 从第2棵树开始，每一棵树的节点是上一棵树的边线。比如，第2棵树有两个节点，分别是（1,2）和（2,3），代表上一棵树中连接变量1和2以及连接变量2和3的边线。

• 从第2棵树开始，每一条边线连接的两个节点对应的上一棵树的两条边线必须仅共享一个节点。还是以第2棵树为例，这棵树只有一条边线，对应的两个节点（1,2）和（2,3），这两个节点在第1棵树中共享节点（变量2），那么该边线就代表“条件copula”\(c_{13|2}\)，其中共享的节点（变量2）作为条件变量。

树结构图中每一棵树的边线代表一个二维copula，将这些copula相乘就得到了多维copula的分解公式。

三维copula概率密度有3种可能的分解方式。除了 式 15 以外，第2种分解公式是 \[ c(F_1(x_1),F_2(x_2),F_3(x_3)) = c_{12|3}(F_{1|3}(x_1|x_3),F_{2|3}(x_2|x_3)|x_3)c_{13}(F_1(x_1),F_3(x_3))c_{23}(F_2(x_2),F_3(x_3)), \] 对应的树结构图为

library(VineCopula)
rvm <- RVineMatrix(Matrix = matrix(c(2, 0, 0,
                                     1, 1, 0,
                                     3, 3, 3), 3, 3, byrow = TRUE))
par(mfrow = c(1,2))
plot(rvm, tree = 1)
plot(rvm, tree = 2)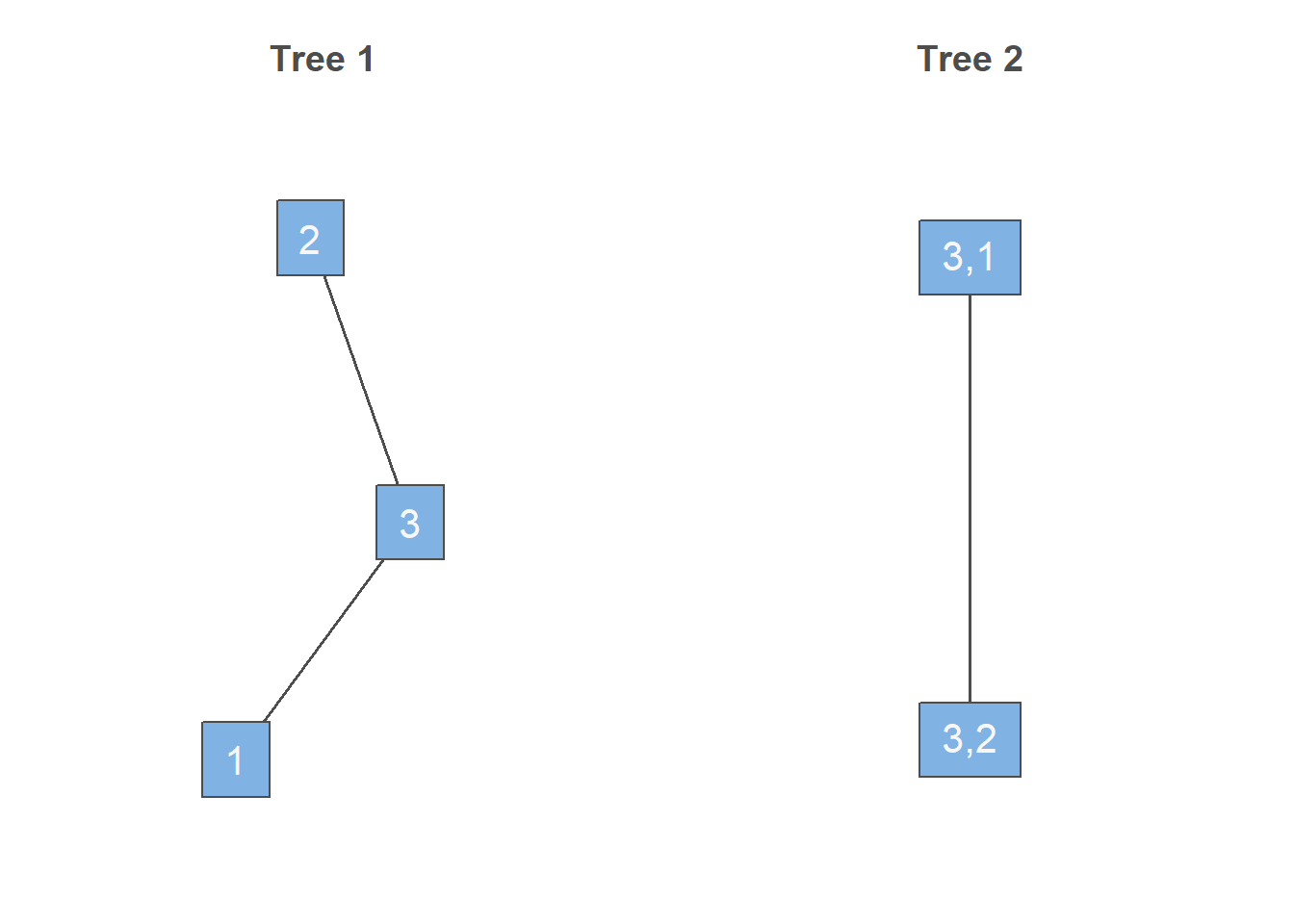

第3种分解公式是 \[ c(F_1(x_1),F_2(x_2),F_3(x_3)) = c_{23|1}(F_{2|1}(x_2|x_1),F_{3|1}(x_3|x_1)|x_1)c_{13}(F_1(x_1),F_3(x_3))c_{12}(F_1(x_1),F_2(x_2)) \] 相应的树结构图为

library(VineCopula)
rvm <- RVineMatrix(Matrix = matrix(c(3,2,1,0,2,1,0,0,1),3,3))
par(mfrow = c(1,2))
plot(rvm, tree = 1)
plot(rvm, tree = 2)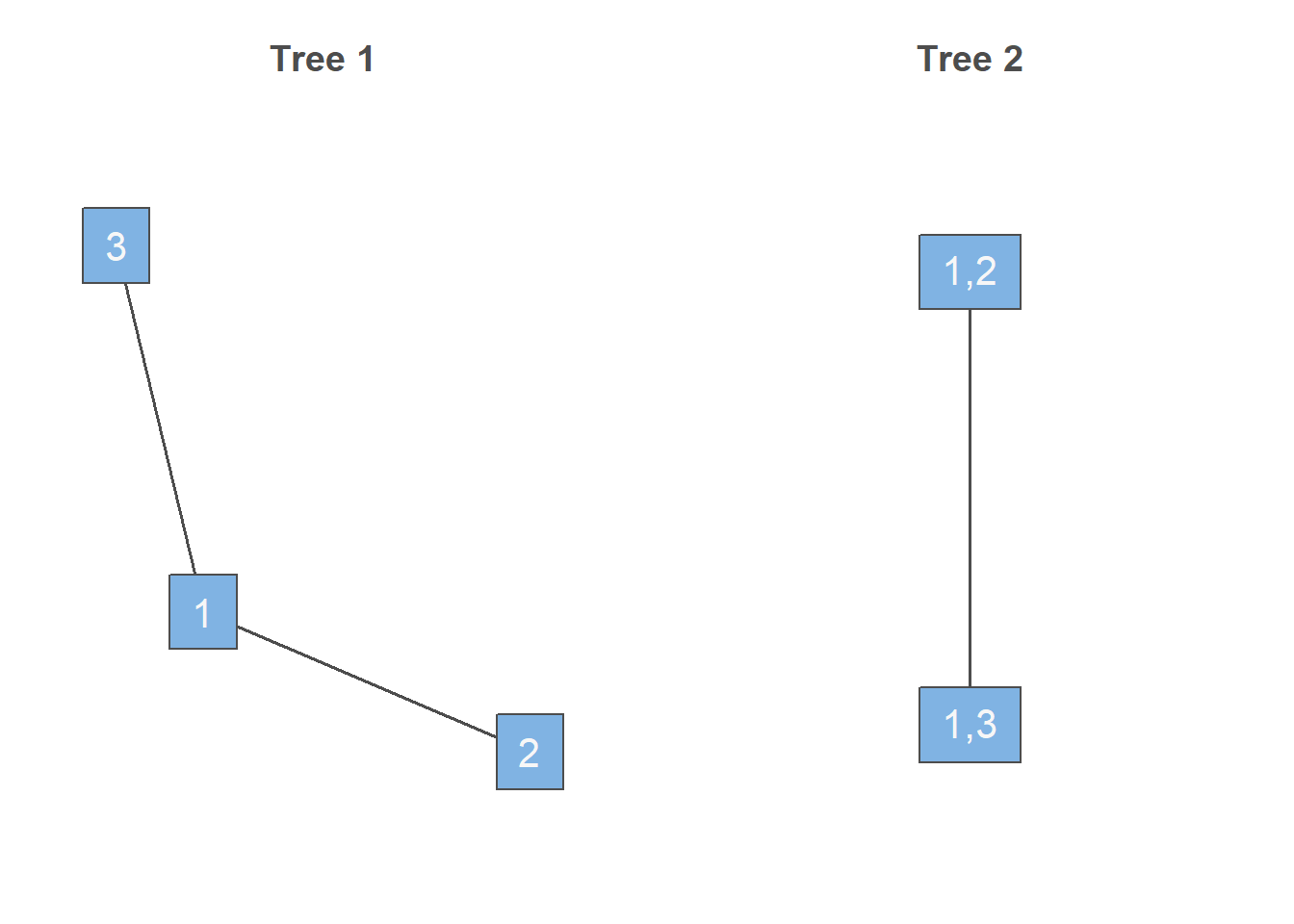

3.3 Vine copula的简化假设与参数估计

我们结合三维copula分解 式 15 介绍vine copula估计中必要的简化假设和参数估计过程。注意到 式 15 中包含条件copula \[ c_{13|2}(F_{1|2}(x_1|x_2),F_{3|2}(x_3|x_2)|x_2), \] 代表条件分布\((X_1,X_3)|X_2=x_2\)的copula密度函数。一般来说，当\(x_2\)的值发生变化时，条件分布发生改变，那么条件copula \(c_{13|2}\)的函数形式也会随着\(x_2\)发生变化，这无疑增加了建模的复杂度。为了解决这一问题，vine copula建模一般做如下简化假设：条件copula的形式不随条件变量值的变化而变化。在该假设下，条件copula \(c_{13|2}(F_{1|2}(x_1|x_2),F_{3|2}(x_3|x_2)|x_2)\)退化为\(c_{13|2}(F_{1|2}(x_1|x_2),F_{3|2}(x_3|x_2))\)，因此分解公式 式 15 写作 \[ c(F_1(x_1),F_2(x_2),F_3(x_3)) = c_{13|2}(F_{1|2}(x_1|x_2),F_{3|2}(x_3|x_2))c_{23}(F_2(x_2),F_3(x_3))c_{12}(F_1(x_1),F_2(x_2)), \] 此时，\(c_{13|2}\)以及\(c_{12},\;c_{23}\)均成为了严格意义上的二维copula建模问题。

给定copula分解的R-vine结构，接下来我们对每一个二维copula做类型假设，分别记为\(c_{13|2}(\cdot,\cdot;\theta_{13|2})\)，\(c_{12}(\cdot,\cdot;\theta_{12})\)和\(c_{23}(\cdot,\cdot;\theta_{23})\)，其中\(\theta_{13|2}\)，\(\theta_{12}\)和\(\theta_{23}\)是各自copula中的未知参数。我们的主要任务是基于独立同分布样本\(\{(X_{1t},X_{2t},X_{3t}):\; t=1,\cdots,n\}\)估计出这些未知参数。估计过程可以根据vine结构中树的顺序依次开展。

• 估计第1棵树中的copula，即\(c_{12}\)和\(c_{23}\)。这一步骤较为简单，可以直接使用二维copula估计方法。记\(\hat F_1\)，\(\hat F_2\)和\(\hat F_3\)分别为三个变量的经验分布函数，作为边缘分布函数\(F_1\)，\(F_2\)和\(F_3\)的估计。以估计\(c_{12}\)为例，我们可以使用最大似然法估计出\(\hat \theta_{12}\)，即 \[ \hat \theta_{12} = \arg\max_{\theta_{12}} \sum_{t=1}^n \log c_{12}(\hat U_{1t},\hat U_{2t}; \theta_{12}), \] 其中\(\hat U_{1t} = \hat F_1(X_{1t})\)，\(\hat U_{2t} = \hat F_2(X_{2t})\)。类似地，我们得到\(\hat \theta_{23}\)，即\(c_{23}\)的估计。

• 估计第2棵树中的copula，即\(c_{13|2}\)。这一步骤稍微复杂一些，主要原因是需要寻找条件分布函数\(F_{1|2}\)和\(F_{3|2}\)的估计。在此之前，我们首先引入H-函数的定义。对于一个二维copula函数\(C(u,v)\)，定义两个H-函数： \[ \begin{aligned} H(u|v) &:= P(U \leq u | V = v) = \frac{\partial C(u,v)}{\partial v} = \int_0^u c(\omega,v)d\omega \\ H(v|u) &:= P(V \leq v | U = u) = \frac{\partial C(u,v)}{\partial u}= \int_0^v c(u,\omega)d\omega. \end{aligned} \] 常用copula的H-函数可以很方便地通过VineCopula包进行计算。H-函数这一概念与条件分布紧密相关，以\(F_{1|2}\)为例，我们有 \[ \begin{aligned} F_{1|2}(x_1|x_2) &= \int_{-\infty}^{x_1} f_{1|2}(z|x_2)dz = \int_{-\infty}^{x_1} \frac{f_{12}(z,x_2)}{f_2(x_2)} dz \\ &= \int_{-\infty}^{x_1} c_{12}(F_1(z),F_2(x_2))f_1(z)dz \quad \quad \quad \text{变量替换：}\omega=F_1(z) \\ &= \int_0^{F_1(x_1)}c_{12}(\omega,F_2(x_2))d\omega \\ &= H_{12}(F_1(x_1)|F_2(x_2)), \end{aligned} \] 其中\(H_{12}\)代表\(c_{12}\)所对应的H-函数。由于在上一棵树的copula估计中得到了\(\hat c_{12}\)，那么我们可以很方便地估计出 \[ \hat F_{1|2}(X_{1t}|X_{2t}) = H_{12}(\hat F_1(X_{1t})|\hat F_2(X_{2t});\hat \theta_{12}). \tag{16}\] 同样地，我们还有 \[ \hat F_{3|2}(X_{3t}|X_{2t}) = H_{23}(\hat F_3(X_{3t})|\hat F_2(X_{2t});\hat \theta_{23}), \tag{17}\] 这里所需要的\(c_{23}\)的估计也能从上一棵树中获得。在取得条件分布函数的估计后，第2棵树中未知的\(c_{13|2}\)可以通过最大似然估计： \[ \hat \theta_{13|2} = \arg\max_{\theta_{13|2}} \sum_{t=1}^n \log c_{13|2}(\hat F_{1|2}(X_{1t}|X_{2t}),\hat F_{3|2}(X_{3t}|X_{2t});\theta_{13|2}). \]

3.4 模型选择

Vine copula涉及两个层面的模型选择问题。第一，给定vine结构，如何确定每一个二维copula的具体类型？这个问题可以通过AIC或者BIC进行选择。第二，如何确定vine结构？这个问题更为困难。随着维度增加，可行的vine结构数量迅速膨胀，我们无法穷尽每一种可能进行比较。当前的主流做法是使用Dissmann et al (2013)的结构选择算法。

Dissmann算法的核心思想是贪婪选择策略，即优先拟合最强依赖关系，并通过逐层筛选构建简化模型结构。具体步骤可以简单概括为

• 构建第1棵树。以任意两变量间的经验Kendall’s tau绝对值作为权重，使用最大生成树算法（Maximal Spanning Tree）选择依赖最强的边构建树1，并为每条边选择二元Copula族并估计参数。

• 构建后续树（如树2）。根据邻近条件（Proximity Condition），从前一棵树中筛选允许连接的边。基于类似于 式 16 或者 式 17 所生成的伪数据计算候选边对应的条件经验Kendall’s tau绝对值作为权重，再次应用最大生成树算法构建树2，为树2中的边选择Copula族并估计参数。

• 重复上述步骤，逐层构建所有树，直至完成。

Dissmann算法可通过VineCopula包高效实现。

3.5 实际应用

我们选择5个行业，每个行业挑选出其中的龙头股，然后基于5支股票近5年日度收益率数据拟合vine copula。这5支股票是：

• 银行/金融：工商银行

• 白酒/消费：贵州茅台

• 新能源：宁德时代

• 科技/半导体：中芯国际

• 家电/消费：美的集团

library(pedquant)    
library(quantmod)
library(tidyverse)
library(VineCopula)


# 获取上证综指和创业板数据
dat <- md_stock(
  symbol = c("601398.sh","600519.sh","300750.sz","688981.sh","000333.sz"), 
  date_range = "5y", 
  source = "163",    # 网易财经数据源
  adjust = "hfq"     # 后复权处理
) 

1/5 601398.sh
2/5 600519.sh
3/5 300750.sz
4/5 688981.sh
5/5 000333.sz

# 计算日度收益率
dat <- lapply(dat, function(df) {
  df$date <- as.Date(df$date)
  # 创建xts对象
  df <- xts(df$close_adj, order.by = df$date)
  # 计算收益率
  periodReturn(df, period = 'daily', type = "log")
})


# 按照日期合并
dat <- reduce(dat, .f = merge.xts, join = 'inner')
colnames(dat) <- c("工商银行","贵州茅台","宁德时代","中芯国际","美的集团")

# 显示数据的前5行
head(dat)

               工商银行     贵州茅台     宁德时代     中芯国际      美的集团
2020-07-16 -0.002463055 -0.078725768 -0.050737669  0.000000000 -0.0266055175
2020-07-17  0.000000000  0.019931869 -0.005442675 -0.073291948  0.0396474548
2020-07-20  0.008594282 -0.006447820  0.047803585  0.027013100  0.0478490011
2020-07-21 -0.003674223  0.017944909  0.008232093 -0.006844133 -0.0003939052
2020-07-22 -0.001227747  0.005758875  0.004282868  0.011883831  0.0000000000
2020-07-23 -0.007398307 -0.001185446  0.026582314 -0.009977980  0.0374351769

# 使用经验分布对样本进行变换
dat <- apply(dat, MARGIN = 2, FUN = function(z) rank(z)/(length(z)+1))


# vine copua拟合
rvm <- RVineStructureSelect(data = dat, familyset = NA)

# 绘制树结构图
par(mfrow = c(2,2))
plot(RVineMatrix(rvm$Matrix), tree = 1)
plot(RVineMatrix(rvm$Matrix), tree = 2)
plot(RVineMatrix(rvm$Matrix), tree = 3)
plot(RVineMatrix(rvm$Matrix), tree = 4)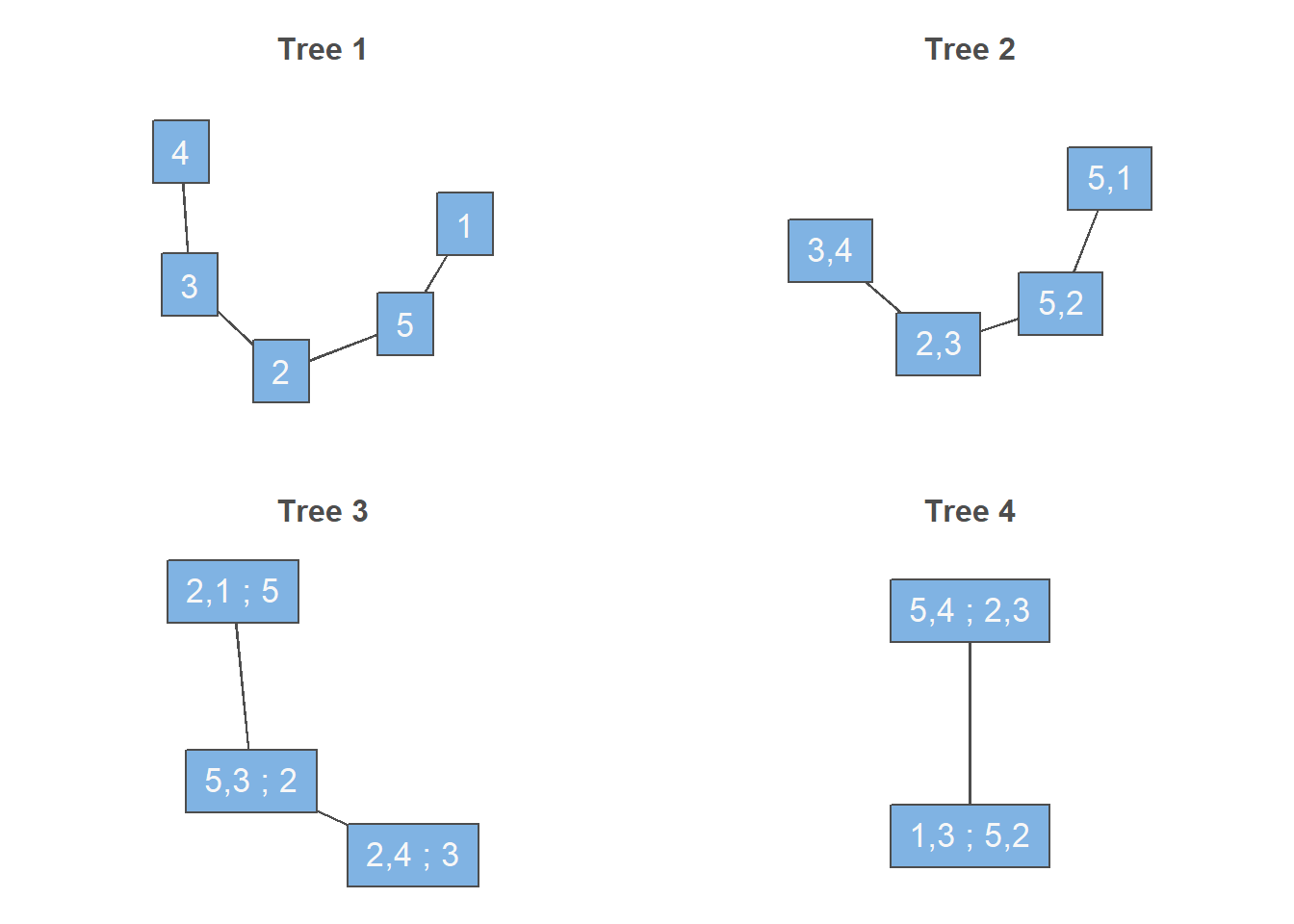

# 显示每一个二维copula估计
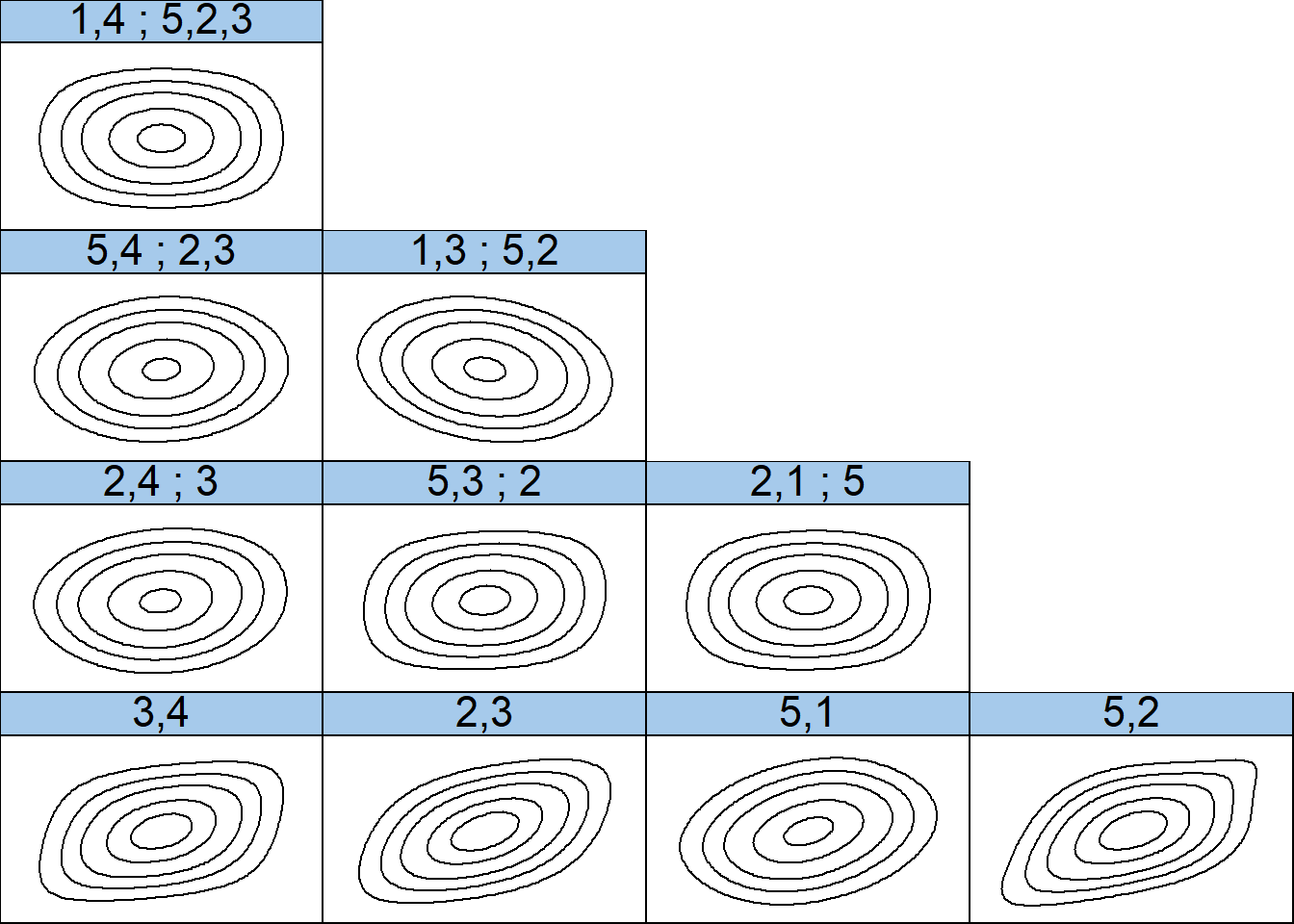
summary(rvm)

tree       edge | family  cop    par  par2 |   tau   utd   ltd 
-------------------------------------------------------------- 
   1        3,4 |      2    t   0.28  5.69 |  0.18  0.10  0.10
            2,3 |      2    t   0.42  8.36 |  0.27  0.08  0.08
            5,1 |      5    F   1.45  0.00 |  0.16     -     -
            5,2 |      9  BB7   1.25  0.54 |  0.29  0.26  0.28
   2      2,4;3 |     10  BB8   1.28  0.80 |  0.06     -     -
          5,3;2 |      2    t   0.10  8.10 |  0.06  0.02  0.02
          2,1;5 |      2    t   0.04  9.48 |  0.03  0.01  0.01
   3    5,4;2,3 |      5    F   0.40  0.00 |  0.04     -     -
        1,3;5,2 |      1    N  -0.17  0.00 | -0.11     -     -
   4  1,4;5,2,3 |      2    t   0.00  9.55 |  0.00  0.01  0.01
---
type: D-vine    logLik: 392.4    AIC: -750.79    BIC: -665.15    
---
1 <-> 工商银行,   2 <-> 贵州茅台,   3 <-> 宁德时代,   4 <-> 中芯国际,   5 <-> 美的集团

contour(rvm)