第七讲: 非线性回归函数

class: center, middle, inverse, title-slide

.title[
# 第七讲: 非线性回归函数
]
.author[
### 文旷宇
]
.institute[
### 华中科技大学
]

---

<div>
<style type="text/css">.xaringan-extra-logo {
width: 55px;
height: 64px;
z-index: 0;
background-image: url(../images/hust-logo.png);
background-size: contain;
background-repeat: no-repeat;
position: absolute;
top:1em;right:1em;
}
</style>
<script>(function () {
  let tries = 0
  function addLogo () {
    if (typeof slideshow === 'undefined') {
      tries += 1
      if (tries < 10) {
        setTimeout(addLogo, 100)
      }
    } else {
      document.querySelectorAll('.remark-slide-content:not(.title-slide):not(.inverse):not(.hide_logo)')
        .forEach(function (slide) {
          const logo = document.createElement('div')
          logo.classList = 'xaringan-extra-logo'
          logo.href = null
          slide.appendChild(logo)
        })
    }
  }
  document.addEventListener('DOMContentLoaded', addLogo)
})()</script>
</div><script>document.addEventListener('DOMContentLoaded',function(){new xeBanner(JSON.parse('{"left":"","right":"","exclude":["title-slide"],"position":"top"}'))})</script>
<script>document.addEventListener('DOMContentLoaded',function(){new xeBanner(JSON.parse('{"left":"文旷宇/华中科技大学","exclude":["title-slide"],"position":"bottom"}'))})</script>

### 主要内容
- 非线性回归函数的一般建模方法
 - 使用的数据集：测试成绩和地区收入
 
 - 非线性设定形式中 `$X$` 变化对 `$Y$` 的效应
- 一元非线性函数
 - 多项式
 
 - 对数

- 自变量的交互作用
 - 两个二值变量的交互作用
 
 - 连续变量和二值变量的交互作用
 
 - 两个连续变量的交互作用
---

### 非线性回归函数的一般建模方法
.panelset[
.panel[.panel-name[注]
- 在我们熟悉的加利福尼亚学区分数的例子中，学生的经经济背景是解释标准化测试成绩一个重要原因

- 利用加利福尼亚数据集中五年级学生的测试成绩对地区收入作散点图 `$8.1$` 及连接两个变量的OLS回归线

- 由图可见:

- 测试成绩和平均收入之间呈强正相关关系，相关系数为0.71，表明来自富裕地区的学生比贫困地区学生的测试成绩更好

- 但是收入很低（10000美元以下）或很高（40000美元以上）时大部分回归点在OLS线之下，收入在15000美元和30000美元之间时落在回归线之上

- 测试成绩和收入之间存在线性回归无法刻画的曲线关系
]
.panel[.panel-name[]
.panel[.panel-name[Code]

```r
# 准备数据
library(AER)               
data(CASchools)
CASchools$size <- CASchools$students/CASchools$teachers
CASchools$score <- (CASchools$read + CASchools$math) / 2       
# 拟合一个简单的线性模型
# 利用CASchools数据集，作成绩对收入的回归拟合图像
linear_model<- lm(score ~ income, data = CASchools)

# 利用观测值作散点图
plot(CASchools$income, CASchools$score,
     col = "steelblue",
     pch = 20,
#pch取15~20时点为实心点，可用col参数设置其填充的颜色
     xlab = "District Income (thousands of dollars)", 
     ylab = "Test Score",
#labs函数是标度函数，可以设置坐标轴和图例上的标签，可以是字符串或数学表达值
     cex.main = 0.9,
#cex：表示相对于默认大小缩放倍数的数值。cex.main：标题的缩放倍数。
     main = "Test Score vs. District Income and a Linear OLS Regression Function")

# 在散点图上添加回归线
abline(linear_model, 
       col = "red", 
       lwd = 2)
# abline函数用于在图形中添加一条或多条直线，lwd设置线宽。#legend函数设置图例，legend参数是字符/表达式向量
legend("bottomright", legend="linear fit",lwd=2,col="red")
```

]

.panel[.panel-name[Output]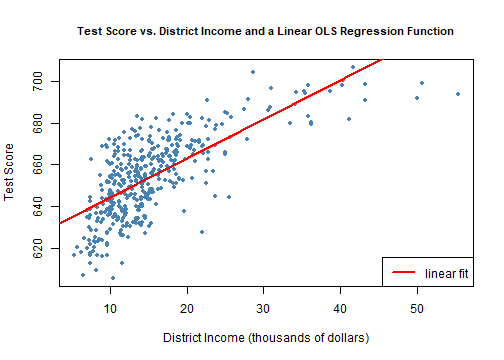

![](Lecture_7_Nonlinear_Regression_files/figure-html/unnamed-chunk-2-1.png)

]
]]
---

### 非线性回归函数的一般建模方法
.panelset[
.panel[.panel-name[注]
- 函数 `$f(X)$` 的斜率依赖 `$X$` 的取值，是非线性的

- 图 `$8.1$` 曲线在收入较低时较陡，在收入走高时较平坦，于是用二次函数模拟该关系
`$$TestScore_i=\beta_0+\beta_1Income_i+\beta_2Income_i^2+u_i$$`

- 由于总体系数未知，我们不能根据平均收入预测学区的测试成绩，必须利用样本数据进行估计

- 上式定义了两个回归变量 `$Income_i$` 、 `$Income_i^2$` ,非线性回归模型是包含两个回归变量的多元回归模型。

- 由420个观测值和OLS估计可知
`$$\hat TestScore=607.3+3.85Income-0.0423Income^2,\bar R^2=0.554$$`
]
.panel[.panel-name[]
.panel[.panel-name[Code]

```r
# 准备数据
library(AER)               
data(CASchools)
CASchools$size <- CASchools$students/CASchools$teachers
CASchools$score <- (CASchools$read + CASchools$math) / 2

# 拟合二次模型
quadratic_model <- lm(score ~ income + I(income^2), data = CASchools)

# 模型系数总结
#lmtest包中的coeftest函数对回归模型中的每个估计系数执行 t 检验。
coeftest(quadratic_model, vcov. = vcovHC, type = "HC1")
```

]

.panel[.panel-name[Output]

```
## 
## t test of coefficients:
## 
##                Estimate  Std. Error  t value  Pr(>|t|)    
## (Intercept) 607.3017435   2.9017544 209.2878 < 2.2e-16 ***
## income        3.8509939   0.2680942  14.3643 < 2.2e-16 ***
## I(income^2)  -0.0423084   0.0047803  -8.8505 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

]
]]
---

### 非线性回归函数的一般建模方法
.panelset[
.panel[.panel-name[注]
- 这个二次模型让我们可以检验测试分数和地区收入是线性关系的原假设和二者是二次关系的备择假设
`$$H_0:\beta_2=0 \qquad H_1:\beta \ne 0$$`
$$
`\begin{aligned}
t&=(\hat \beta_2-0)/SE(\hat \beta_2)\\
&=-0.0423/0.0048\\
&=-8.81\\
&<-1.96\\
\end{aligned}`
$$ 
可在95%显著水平下拒绝原假设

- 于是在图 `$8.1$` 线性回归基础上作二次回归模型图
]
.panel[.panel-name[]
.panel[.panel-name[Code]

```r
# 准备数据
library(AER)               
data(CASchools)

CASchools$size <- CASchools$students/CASchools$teachers
CASchools$score <- (CASchools$read + CASchools$math) / 2
# 拟合一个简单的线性模型
# 利用CASchools数据集，作成绩对收入的回归拟合图像
linear_model<- lm(score ~ income, data = CASchools)
# 绘制收入和测试分数观测值的散点图
plot(CASchools$income, CASchools$score,
     col  = "steelblue",
     pch = 20,
#pch取15~20时点为实心点，可用col参数设置其填充的颜色
     xlab = "District Income (thousands of dollars)",
     ylab = "Test Score",
#labs函数是标度函数，可以设置坐标轴和图例上的标签，可以是字符串或数学表达值
     main = "Estimated Linear and Quadratic Regression Functions")

# 在图中添加线性函数
abline(linear_model, col = "green", lwd = 2)
# abline函数用于在图形中添加一条或多条直线，lwd设置线宽。

# 在图中添加四分函数
order_id <- order(CASchools$income)
# order函数默认用于返回向量从小到大排序在原始向量中的位次（秩）。

lines(x = CASchools$income[order_id], 
      y = fitted(quadratic_model)[order_id],
      col = "red", 
      lwd = 2) 
#legend函数设置图例，legend参数是字符/表达式向量
legend("bottomright",legend=c("Linear Line","Quadratic Line"),
       lwd=2,col=c("green","red"))
```

]

.panel[.panel-name[Output]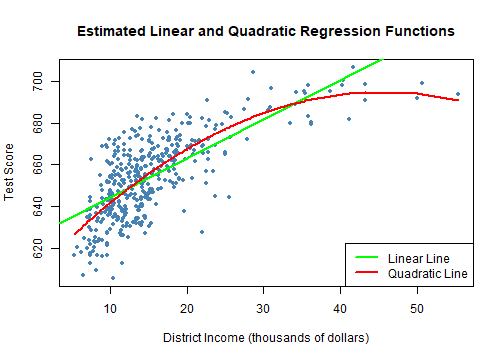

![](Lecture_7_Nonlinear_Regression_files/figure-html/unnamed-chunk-4-1.png)

]
]
]
---

### 非线性回归函数
- 之前学习的线性函数
`$$Y_i=\beta_0+\beta_1X_{1,i}+\beta_2X_{2,i}+···+\beta_kX_{k,i}+u_i$$`
- 自变量 `$X_j$` 改变一单位对 `$Y_i$` 的影响固定不变，恒等于 `$\beta_j$`

- 非线性函数中， `$X$` 的变化对 `$Y$` 的效应依赖于一个或多个自变量的取值

- 回归模型是独立变量 `$X_{1,i},······,X_{k,i}$` 的非线性函数
 
     - 类似多元回归模型，可用OLS估计

- 回归模型是未知系数 `$\beta_0,\beta_1,···,\beta_k$` 的非线性函数
 
     - 不能用OLS估计
     
- 我们主要学习第一种
---

### 非线性回归函数
`$$Y_i=f(X_{1,i},X_{2,i},···,X_{k,i})+u_i$$`
.panelset[
.panel[.panel-name[1]
- 四个假设
 - `$E(u_i|(X_{1,i},X_{2,i},···,X_{k,i})=0,$` 即 `$f$` 是给定 `$X$` 时 `$Y$` 的条件期望
 
 - `$(X_{1,i},X_{2,i},···,X_{k,i},Y_i)$` 独立同分布
 
 - 大的异常值不太可能出现
 
 - 不完全多重共线性
]
.panel[.panel-name[2]
- `$X_1$` 变化对 `$Y$` 的效应

- 自变量 `$X_1$` 的变化对 `$Y$`的效应依赖于 `$X_1$` 自身的取值
     - 如降低班级规模 `$X$` 一个单位对成绩 `$Y$` 的影响在 `$X$` 很小（小到便于管理时）比很大（以至于老师仅能维持班级次序时）大

- 自变量 `$X_1$` 的变化对 `$Y$` 的效应依赖于其他变量如 `$X_2$`
     - 如学区英语学习者比率的影响
]]
---

###一元非线性函数-多项式
- 下面介绍非线性回归函数的两种建模方法(只讨论涉及一个自变量 `$X$` )

- **多项式**

- 利用 `$X$` 的多项式确定非线性回归函数，令 `$r$` 表示回归中 `$X$` 的最高次方，则 `$r$` 阶多项式回归模型
 `$$Y_i=\beta_0+\beta_1X_i+\beta_2X_i^2+···+\beta_rX_i^r+u_i$$`
 - 这里回归变量不是不同的变量，而是同一自变量 `$X$` 的不同次方即 `$X,X^2,X^3$` 等等

- 检验总体回归函数是线性的原假设——** `$F$` 统计量**
`$$H_0:\beta_2=0,···,\beta_r=0
\qquad H_1:\text{至少有一个}\beta_j \ne 0,j=2,3,···,r$$`
- 多项式回归中系数最佳解释

- 画出回归函数估计图并计算 `$X$` 变化对 `$Y$` 的效应估计
---

###一元非线性函数-多项式
- 应该采用的多项式阶数
 - 需要权衡灵活性和统计精确度
    
     - 提高阶数 `$r$` 使回归模型更具灵活性，可以匹配更多的形态（ `$r$` 阶多项式可以有直到 `$r-1$` 的弯曲即拐点）
     
     - 提高阶数 `$r$` 意味着加入了更多回归变量，会降低估计的精确度
 - 顺序假设检验
 
     - 选定最大的 `$r$` 值并估计 `$r$` 阶多项式回归
     
     - `$t$` 统计量检验 `$X^r$` 系数为0的假设
     
     - 若不能拒绝 `$\beta_r=0$` 的假设，则剔除 `$X^r$` 并估计 `$r-1$` 阶多项式回归，若拒绝则使用 `$r-1$` 阶多项式
     
     - 检验 `$\beta_{r-1}=0,$` 重复至最高次方的系数统计显著
 - 实际应用中非线性函数大多光滑，选择较小的 `$r$` 较合适
---

###仿真模拟
.panelset[
.panel[.panel-name[]
.panel[.panel-name[F检验]

```r
# 估计一个立方模型，设置 raw = TRUE，以便计算原始多项式
cubic_model <- lm(score ~ poly(income, degree = 3, raw = TRUE), data = CASchools)

# 根据二次式或多项式检验线性模型的假设
# 备择假设
# 设置假设矩阵
R <- rbind(c(0, 0, 1, 0),
            c(0, 0, 0, 1))

# 进行检验
linearHypothesis(cubic_model,hypothesis.matrix=R,white.adj = "hc1")
```

]

.panel[.panel-name[Output]

```
## Linear hypothesis test
## 
## Hypothesis:
## poly(income, degree = 3, raw = TRUE)2 = 0
## poly(income, degree = 3, raw = TRUE)3 = 0
## 
## Model 1: restricted model
## Model 2: score ~ poly(income, degree = 3, raw = TRUE)
## 
## Note: Coefficient covariance matrix supplied.
## 
##   Res.Df Df      F    Pr(>F)    
## 1    418                        
## 2    416  2 37.691 9.043e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

]
]
.panel[.panel-name[]
.panel[.panel-name[3阶系数检验]

```r
# t检验
# 使用稳健的标准误检验假设，拒绝回归函数是二次函数的原假设
coeftest(cubic_model, 
#表示要进行检验的对象，—般需是一个回归模型(即lm类型数据)
         vcov. = vcovHC, 
#vcov.表示参数的方差(矩阵)，当取默认值NULL时，使用的就是传统回归的估计方法，vcovHC是包含协方差矩阵估计值的矩阵。
         type = "HC1")
#指定估计类型的字符串，如常数等
```

]

.panel[.panel-name[Output]

```
## 
## t test of coefficients:
## 
##                                          Estimate  Std. Error  t value  Pr(>|t|)    
## (Intercept)                            6.0008e+02  5.1021e+00 117.6150 < 2.2e-16 ***
## poly(income, degree = 3, raw = TRUE)1  5.0187e+00  7.0735e-01   7.0950 5.606e-12 ***
## poly(income, degree = 3, raw = TRUE)2 -9.5805e-02  2.8954e-02  -3.3089  0.001018 ** 
## poly(income, degree = 3, raw = TRUE)3  6.8549e-04  3.4706e-04   1.9751  0.048918 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

]
]
.panel[.panel-name[]
.panel[.panel-name[F检验]

```r
#进行稳健的F-test 
linearHypothesis(cubic_model, hypothesis.matrix = R,vcov. = vcovHC, type = "HC1")
```

]

.panel[.panel-name[Output]

```
## Linear hypothesis test
## 
## Hypothesis:
## poly(income, degree = 3, raw = TRUE)2 = 0
## poly(income, degree = 3, raw = TRUE)3 = 0
## 
## Model 1: restricted model
## Model 2: score ~ poly(income, degree = 3, raw = TRUE)
## 
## Note: Coefficient covariance matrix supplied.
## 
##   Res.Df Df      F    Pr(>F)    
## 1    418                        
## 2    416  2 29.678 8.945e-13 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

]
]]
---

###一元非线性函数-对数
- 对数变换将变量化为百分率变化，用百分率可以很容易地表示多种关系式
 - 如工资用百分率表示比美元表示更容易比较工资在职业和时间上的差距
 
 - 前面我们发现地区收入和测试成绩间是非线性相关的，如果用百分率表示呢？
 
 - 地区收入变化1%而不是1000美元时引起的测试成绩变化对不同收入的取值近似不变吗？
 
 - 通常称价格上涨1%导致的需求量下降百分率为**价格弹性**
 
- **对数和百分率**
`$$ln(X+\Delta X)-ln(X)=ln(1+\frac{\Delta X}{X}) \approx \frac{\Delta X}{X}, \qquad (\frac{\Delta X}{X}\text{很小时})$$`
---

###三种对数回归模型-线性对数模型
- **线性对数模型**

- `$X$` 是对数形式而 `$Y$` 不是
`$$Y_i=\beta_0+\beta_1ln(X_i)+u_i$$`
 - *** `$X$` 变化1%引起 `$Y$` 的变化为 `$0.01\beta_1$` ***
`$$[\beta_0+\beta_1ln(X+\Delta X)]-[\beta_0+\beta_1ln(X)]\approx \beta_1(\frac{\Delta X}{X}),\qquad (\frac{\Delta X}{X}\text{很小时})$$` 
 - 在地区收入和测试成绩的实例中
`$$\hat{TestScore}=557.8+36.42ln(Income),\bar{R^2}=0.561$$`
     - 由上式知收入增加 `$1 \%$` 时测试成绩提高 `$0.01 \times36.42 \approx 0.36$` (分)
---

###仿真模拟-线性对数模型
.panelset[
.panel[.panel-name[]
.panel[.panel-name[Code]

```r
# 估计一个线性对数模型并进行t检验
LinearLog_model <- lm(score ~ log(income), data = CASchools)
#与多项式回归类似，我们不必在使用lm之前创建新变量。我们可以简单地调整lm的公式参数来告诉 R 应该使用变量的对数转换。

# 计算稳健的系数summary
#lmtest包中的coeftest函数对回归模型中的每个估计系数执行 t/z 检验。
coeftest(LinearLog_model, 
#表示要进行检验的对象，—般需是一个回归模型(即lm类型数据)
         vcov = vcovHC,
#vcov.表示参数的方差(矩阵)，当取默认值NULL时，使用的就是传统回归的估计方法

#df表示t检验的自由度，当取默认值NULL时，自由度为n-k(即样本量减参数量)，而当df取负值时，检验方法将会从t检验(t分布假设)变为z检验(正态分布假设)。
         type = "HC1")
```

]

.panel[.panel-name[Output]

```
## 
## t test of coefficients:
## 
##             Estimate Std. Error t value  Pr(>|t|)    
## (Intercept) 557.8323     3.8399 145.271 < 2.2e-16 ***
## log(income)  36.4197     1.3969  26.071 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

]
]
.panel[.panel-name[]
.panel[.panel-name[Code]

```r
# 画出函数图
plot(score ~ income, 
     col = "steelblue",
     pch = 20,
#pch取15~20时点为实心点，可用col参数设置其填充的颜色
     data = CASchools,
     ylab="Score",
     xlab="Income",
#labs函数是标度函数，可以设置坐标轴和图例上的标签，可以是字符串或数学表达值
     main = "Linear-Log Regression Line")

# 添加线性对数回归线
# order函数默认用于返回向量从小到大排序在原始向量中的位次（秩）。
order_id  <- order(CASchools$income)
#line(x,y)函数实现线性拟合，并返回截距项和斜率项。lines函数是一个低级绘图函数，可以在plot的绘图区域中添加点或线。
lines(CASchools$income[order_id],
      fitted(LinearLog_model)[order_id], 
      col = "red", 
      lwd = 2)
#legend函数设置图例，legend参数是字符/表达式向量
legend("bottomright",legend = "Linear-log line",lwd = 2,col ="red")
```

]

.panel[.panel-name[Output]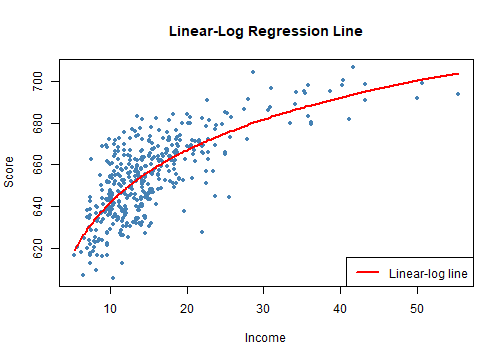

![](Lecture_7_Nonlinear_Regression_files/figure-html/unnamed-chunk-9-1.png)

]
]]
---

###三种对数回归模型-对数线性模型
.panelset[
.panel[.panel-name[注]
- **对数线性模型**

- `$Y$` 是对数形式而 `$X$` 不是
`$$ln(Y_i)=\beta_0+\beta_1X_i+u_i$$`
 - *** `$X$` 变化一个单位( `$\Delta X=1$` )引起 `$Y$` 的变化为 `$100 \times \beta_1 \%$` ***
 `$$ln(Y+\Delta Y)-ln(Y)=\beta_1 \Delta X \approx \frac{\Delta Y}{Y}=100\times\frac{\Delta Y}{Y}\%,\quad (\beta_1 \Delta X \text{很小时})$$`
]
.panel[.panel-name[例]

- 在2009年3月人口调查的实例中
`$$ln(\hat{Earnings})=2.805+0.0087Age,\bar{R^2}=0.027$$`
     - 由上式知年龄每增加 `$1$` 岁时预计收入增加 `$(100 \times0.0087)\%=0.87\%$` 
     
 - 在地区收入和测试成绩的实例中
`$$ln(\hat{TestScore})=6.439+0.003Income$$`
     - 由上式知收入每增加 `$1$` 美元时预计测试成绩提高 `$(100 \times0.003)\%=0.3\%$` 
]]
---

###三种对数回归模型-双对数模型
- **双对数模型**

- `$X,Y$` 都是对数形式
`$$ln(Y_i)=\beta_0+\beta_1ln(X_i)+u_i$$`
 - *** `$X$` 变化 `$1\%$` 引起 `$Y$` 的变化为 `$\beta_1 \%$` ***
$$ln(Y+\Delta Y)-ln(Y)=[\beta_1 ln(X+\Delta X)-ln(X)] $$
`$$\frac{\Delta Y}{Y} \approx \beta_1 \frac{\Delta X}{X},\qquad \beta_1=\frac{\frac{\Delta Y}{Y}}{\frac{\Delta X}{X}}=\frac{100\times\frac{\Delta Y}{Y}}{100\times\frac{\Delta X}{X}}=\frac{Y的百分率变化}{X的百分率变化}$$`
 - 在地区收入和测试成绩的实例中
`$$ln(\hat{TestScore})=6.336+0.055ln(Income),\bar{R^2}=0.557$$`
     - 由上式知收入增加 `$1 \%$` 时预计测试成绩提高 `$0.0554\%$`
---

###仿真模拟-对数线性模型、双对数模型
.panelset[
.panel[.panel-name[]
.panel[.panel-name[Code]

```r
# 估计一个对数线性模型
LogLinear_model <- lm(log(score) ~ income, data = CASchools)
# 估计一个双对数模型
LogLog_model <- lm(log(score) ~ log(income), data = CASchools)

# 输出稳健的系数总结
# 对数线性模型
coeftest(LogLinear_model, 
         vcov = vcovHC, type = "HC1")
# 双对数模型
coeftest(LogLog_model, 
         vcov = vcovHC, type = "HC1")
```

]

.panel[.panel-name[Output]

```
## 
## t test of coefficients:
## 
##               Estimate Std. Error  t value  Pr(>|t|)    
## (Intercept) 6.43936234 0.00289382 2225.210 < 2.2e-16 ***
## income      0.00284407 0.00017509   16.244 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## 
## t test of coefficients:
## 
##              Estimate Std. Error  t value  Pr(>|t|)    
## (Intercept) 6.3363494  0.0059246 1069.501 < 2.2e-16 ***
## log(income) 0.0554190  0.0021446   25.841 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

]
]
.panel[.panel-name[]
.panel[.panel-name[Code]

```r
# 绘制散点图
plot(log(score) ~ income, 
     col = "steelblue", 
#pch取15~20时点为实心点，可用col参数设置其填充的颜色
     pch = 20, 
     data = CASchools,
#labs函数是标度函数，可以设置坐标轴和图例上的标签，可以是字符串或数学表达值
     ylab="log(Score)",
     xlab="Income",
#main函数设置图像标题
     main = "Log-Linear Regression Function")

# 添加对数线性回归线
# order函数默认用于返回向量从小到大排序在原始向量中的位次（秩）。
order_id  <- order(CASchools$income)
#lines函数是一个低级绘图函数，可以在plot的绘图区域中添加点或线。
lines(CASchools$income[order_id], 
      fitted(LogLinear_model)[order_id], 
      col = "red", 
      lwd = 2)

# 添加双对数回归线
lines(sort(CASchools$income), 
      fitted(LogLog_model)[order(CASchools$income)], 
      col = "green", 
      lwd = 2)

# 添加标注
#legend函数设置图例，legend参数是字符/表达式向量
legend("bottomright",
       legend = c("log-linear model", "log-log model"),
       lwd = 2,
       col = c("red", "green"))
```

]

.panel[.panel-name[Output]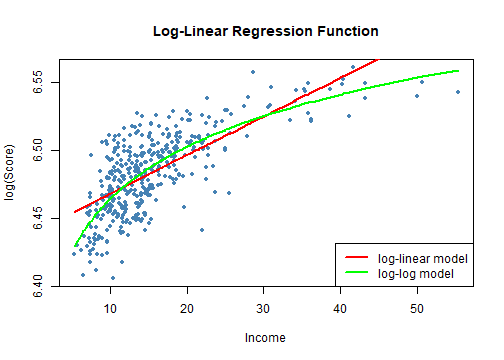

![](Lecture_7_Nonlinear_Regression_files/figure-html/unnamed-chunk-11-1.png)

]
]]
---

###对数设定形式的比较
- 对数线性VS双对数

- 比较 `$\bar R^2$` : `$\bar R^2$` 高的拟合数据的效果好
 
- 线性对数VS线性回归

- 比较 `$\bar R^2$` : `$\bar R^2$` 高的拟合数据的效果好
 
 - 在地区收入和测试成绩的实例中，线性回归 `$\bar R^2=0.561$` ， `$\bar R^2=0.508$` ，因此线性对数模型拟合数据的效果好
 
- 线性对数VS双对数
 - 不能用 `$\bar R^2$` 比较
 
     - `$\bar R^2$`度量了能被回归变量解释的因变量方差比例，而两个回归因变量不同,前者为 `$Y_i$` ，后者为 `$ln(Y_i)$`
     
 - 应该根据经济理论和对问题的实践认知确定用 `$Y$` 的对数形式是否有意义
---

###仿真模拟- `$\bar R^2$` 比较
.panelset[
.panel[.panel-name[]
.panel[.panel-name[Code]

```r
# 估计一个多项式模型
polyLog_model <- lm(score ~ log(income) + I(log(income)^2) + I(log(income)^3), 
data = CASchools)

# 对非线性模型计算调整的 R^2 
adj_R2 <-rbind("quadratic" = summary(quadratic_model)$adj.r.squared,
               "cubic" = summary(cubic_model)$adj.r.squared,
               "LinearLog" = summary(LinearLog_model)$adj.r.squared,
               "LogLinear" = summary(LogLinear_model)$adj.r.squared,
               "LogLog" = summary(LogLog_model)$adj.r.squared,
               "polyLog" = summary(polyLog_model)$adj.r.squared)

# 分配列名
colnames(adj_R2) <- "adj_R2"
adj_R2
```

]

.panel[.panel-name[Output]

```
##              adj_R2
## quadratic 0.5540444
## cubic     0.5552279
## LinearLog 0.5614605
## LogLinear 0.4970106
## LogLog    0.5567251
## polyLog   0.5599944
```

]
]]
---

###仿真模拟-线性对数VS立方（多项式）
.panelset[
.panel[.panel-name[]
.panel[.panel-name[Code]

```r
# 绘制散点图
plot(score ~ income, 
     data = CASchools,
     col = "steelblue", 
     pch = 20,
     ylab="Score",
     xlab="Income",
     main = "Linear-Log and Cubic Regression Functions")

# 添加线性对数回归线
order_id  <- order(CASchools$income)

lines(CASchools$income[order_id],
      fitted(LinearLog_model)[order_id], 
      col = "darkgreen", 
      lwd = 2)

# 添加立方回归线
lines(x = CASchools$income[order_id], 
      y = fitted(cubic_model)[order_id],
      col = "red", 
      lwd = 2)
# 添加图注
legend("bottomright",
       legend = c("Linear-Log model", "Cubic model"),
       lwd = 2,
       col = c("darkgreen", "red"))
```

]

.panel[.panel-name[Output]

![](Lecture_7_Nonlinear_Regression_files/figure-html/unnamed-chunk-13-1.png)

]
]]
---

###当 `$Y$` 为对数形式时 `$Y$` 的预测值计算
- 对数变换
`$$ln(Y_i)=\beta_0+\beta_1X_i+u_i \longrightarrow Y_i=e^{\beta_0+\beta_1X_i}e^{u_i}$$`
- 问题
 - 如果 `$E(u_i|X_i)=0$` , `$E(Y_i|X_i)=e^{\beta_0+\beta_1X_i}E(e^{u_i})$` 
 
 - 但是即使 `$E(u_i)=0,E(e^{u_i})\ne0$`
 
 - 由于遗漏了因子 `$E(e^{u_i})$` ，会导致预测值有偏
- 解决方法
 - 估计因子 `$E(e^{u_i})$` ，然后利用估计值计算 `$Y$` 的预测值
 
 - 计算 `$Y$` 的对数预测值而不转化为原来的单位
---

###自变量的交互作用
- 我们已经知道测试地区收入对成绩的影响

- 现在我们想知道还有很多学生学习英语的学区内降低学生/教师比对测试成绩的效应是否要大于只有少数学生还在学习英语的学区

- 假设两个学区内还在学习英语的学生在一对一或小组辅导中的收获不同

- 那么学区内英语学习者的比例将会与学生/教师比产生交互作用,从而使学生/教师比变化对测试成绩的效应依赖于英语学习者的比例

- **交互作用**
 - 某个自变量对 `$Y$` 的效应依赖于另一个自变量取值
 
 - 如学生/教师比变化对测试成绩的效应依赖于英语学习者的比例
 
 - 分三种情况
     - 两个二值自变量、一个二值自变量与一个连续自变量、两个连续自变量
---

###两个二值自变量的交互作用
- 现实生活中有很多二值变量，如性别，某物的有无等 `$0,1$` 变量
$$
D_{1i}=
`\begin{cases}
0,\quad \text{第i个人为男性}\\
1,\quad \text{第i个人为女性}
\end{cases}`
$$

$$
D_{2i}=
`\begin{cases}
0,\quad \text{第i个人为无大学学位}\\
1,\quad \text{第i个人为大学毕业}
\end{cases}`
$$
- 现在考虑收入对数 ( `$Y_i=ln(Earnings)$` )对性别 `$D_{1,i}$` 和是否拥有大学学位 `$D_{2,i}$` 这两个二值变量的总体回归
`$$Y_i=\beta_0+\beta_1D_{1i}+\beta_2D_{2i}+u_i$$`
 - `$\beta_1$` 表示固定教育程度时，身为女性对收入对数的效应
 
 - `$\beta_2$` 表示性别不变时，拥有大学学位的效应
 
- 该式中固定性别后不论男女拥有大学学位的效应是一样的，但实际生活中劳动市场的文凭价值对男性和女性而言是不同的
---

###两个二值自变量的交互作用
- 上式没有考虑性别和获得大学学位的交互作用

- 我们可以引入另一个取两个二值变量乘积 `$D_{1i}\times D_{2i}$` 的回归变量进行修正，称之为**交互项或交互回归变量**
`$$Y_i=\beta_0+\beta_1D_{1i}+\beta_2D_{2i}+\beta_3(D_{1i}\times D_{2i})+u_i$$`
- 给定 `$D_{1i}$` 取值时
$$
`\begin{aligned}
E(Y_i|D_{1i}&=d_1,D_{2i}=0)=\beta_0+\beta_1 \times d_1+\beta_2 \times 0+\beta_2 \times(d_1\times0)\\
&=\beta_0+\beta_1 d_1
\end{aligned}`
$$
$$
`\begin{aligned}
E(Y_i|D_{1i}=d_1,D_{2i}=1)
&=\beta_0+\beta_1 \times d_1+\beta_2 \times 1+\beta_2 \times(d_1\times1)\\
&=\beta_0+\beta_1 d_1+\beta_2+\beta_3d_1
\end{aligned}`
$$
- 故变化的效应为
`$$E(Y_i|D_{1i}=d_1,D_{2i}=1)-E(Y_i|D_{1i}=d_1,D_{2i}=0)=\beta_2+\beta_3d_1$$`
- 交互项系数 `$\beta_3$` 是女性和男性获得大学学位的效应之差
---

###二值变量交互回归模型的应用
- 在学生/教师比和英语学习者百分率实例中，令
$$
HiSTR_i=
`\begin{cases}
1,\quad \text{学生/教师比}\geq20\\
0,\quad \text{学生/教师比}<20
\end{cases}`
$$ 
$$
HiEL_i=
`\begin{cases}
1,\quad \text{英语学习者百分率}\geq10\%\\
0,\quad \text{英语学习者百分率}<10\%
\end{cases}`
$$ 
- 测试成绩对 `$HiSTR_i,HiEL_i$` 的交互回归为：
`$$\hat{TestScore}=664.1-18.2HiEL-1.9HiSTR-3.5(HiSTR \times HiEL)$$`
`$$\bar R^2=0.290$$`
- 在固定英语学习者百分率的情况下,从低学生/教师比学区变到高学生/教师比学区的效应为 `$-1.9-3.5HiEL$`

- 在固定学生/教师比学区的情况下,从低英语学习者百分率变到高英语学习者百分率的效应为 `$-18.2-3.5HiEL$`

---

###连续变量和二值变量的交互作用
- 考虑收入对数 `$Y_i=ln(Earnings)$` 对工作经验的连续变量 `$X_i$` 和是否拥有大学学位的二值变量 `$D_i$` （第i个人毕业则 `$D_i=1$` ） 
`$$Y_i=\beta_0+\beta_1X_i+\beta_2D_i+u_i$$`
- `$D_i=0$` 时，总体回归函数 `$Y_i=\beta_0+\beta_1X_i$`

- `$D_i=1$` 时，总体回归函数 `$Y_i=\beta_0+\beta_1X_i+\beta_2$`

- 二者斜率相同，截距相差 `$\beta_2$`
 - `$\beta_1$` 为保持大学学位状态不变时增加一年工作经验对收入对数的效应
 
 - `$\beta_2$` 为工作经验保持不变时，大学学位对收入对数的效应
 
- 实际上，大学毕业生和非大学毕业生再工作一年的效应不同，二者斜率应该不同
---

###连续变量和二值变量的交互作用
- 为了使斜率不同，我们可以引入一个交互项
`$$Y_i=\beta_0+\beta_1X_i+\beta_2D_i+\beta_3(X_i\times D_i)+u_i$$`
- `$D_i=0$` 时，总体回归函数 `$Y_i=\beta_0+\beta_1X_i$`

- `$D_i=1$` 时，总体回归函数 `$Y_i=(\beta_0+\beta_2)+(\beta_1+\beta_3)X_i$`

- 二者截距之差为 `$\beta_2$` ，斜率之差为 `$\beta_3$` 
 - `$\beta_1$` 表示非大学毕业生（ `$D_i=0$` ）多一年工作经验的效应，对大学毕业生来说该效应为 `$\beta_1+\beta_3$` 
 
 - `$\beta_3$` 表示多一年工作经验对大学毕业生和非大学毕业生的效应之差
 
- 如果经验在大学毕业生和非大学毕业生之间对收入效应不同，而在没有经验时两组的期望收入对数相同，则二者截距相同，斜率不同
`$$Y_i=\beta_0+\beta_1X_i+\beta_2(X_i\times D_i)+u_i$$`
---

###仿真模拟
.panelset[
.panel[.panel-name[]
.panel[.panel-name[Code]

```r
# 生成人工数据,set.seed设定产生随机数的初始值，用于设定随机数种子，让模拟能够可重复出现，一个特定的种子可以产生一个特定的伪随机序列
set.seed(1)
#使用runif(n,min,max)函数从R中的均匀分布生成随机值。n为生成的随机值的数量，min为分布的最小值（默认为0），max为分布的最大值（默认为1）
X <- runif(200,0, 15)
#随机抽样，sample(x,size,replace = FALSE)中x表示数据范围，size表示抽样数，replace默认FALSE，即抽样数size不能大于x；若为TRUE，size可以大于x
D <- sample(0:1, 200, replace = T)
#设定回归函数Y=450+150X+500D+50(X*D)+u_i
Y <- 450 +  150 * X + 500 * D + 50 * (X * D) + rnorm(200, sd = 300)

# 相应地划分绘图区域,rbind把向量/矩阵纵向合并（行方式）成一个新的向量/矩阵。就是行的叠加，m行的矩阵与n行的矩阵rbind()最后变成m+n行，合并前提是rbind(a, b)中矩阵a、b的列数必需相同。
m <- rbind(c(1, 2), c(3, 0))
#layout函数使排列图形时不再局限于尺寸大小必须相同、页面必须铺满
graphics::layout(m)

# 估计模型并绘制回归线
# 1. (基线模型：相同斜率不同截距)
plot(X, log(Y),
#pch取15~20时点为实心点，可用col参数设置其填充的颜色
     pch = 20,
     col = "steelblue",
#main函数设置图像标题
     main = "Different Intercepts, Same Slope",
#cex.main：标题的缩放倍数。
     cex.main=1.2)

#提取拟合模型的系数赋值给中间量
mod1_coef <- lm(log(Y) ~ X + D)$coefficients

# abline函数用于在图形中添加一条或多条直线，lwd设置线宽。
#回归系数coef即模型参数的估计值
abline(coef = c(mod1_coef[1], mod1_coef[2]), 
       col = "red",
       lwd = 1.5)

abline(coef = c(mod1_coef[1] + mod1_coef[3], mod1_coef[2]), 
       col = "green",
       lwd = 1.5)
       
# 2. (基线模型+交互项：不同斜率不同截距)
plot(X, log(Y),
     pch = 20,
     col = "steelblue",
     main = "Different Intercepts, Different Slopes",
     cex.main=1.2)

mod2_coef <- lm(log(Y) ~ X + D + X:D)$coefficients

abline(coef = c(mod2_coef[1], mod2_coef[2]), 
       col = "red",
       lwd = 1.5)

abline(coef = c(mod2_coef[1] + mod2_coef[3], mod2_coef[2] + mod2_coef[4]), 
       col = "green",
       lwd = 1.5)

# 3. (遗漏回归变量D+交互项：截距相同斜率不同)
plot(X, log(Y),
     pch = 20,
     col = "steelblue",
     main = "Same Intercept, Different Slopes",
     cex.main=1.2)

mod3_coef <- lm(log(Y) ~ X + X:D)$coefficients

abline(coef = c(mod3_coef[1], mod3_coef[2]), 
       col = "red",
       lwd = 2)

abline(coef = c(mod3_coef[1], mod3_coef[2] + mod3_coef[3]), 
       col = "green",
       lwd = 2)
```

]

.panel[.panel-name[Output]

![](Lecture_7_Nonlinear_Regression_files/figure-html/unnamed-chunk-14-1.png)

]
]]
---

###交互项在学生/教师比和英语学习者百分率中的应用
.panelset[
.panel[.panel-name[]
.panel[.panel-name[Code]

```r
# 附加 HiSTR 到 CASchools
#as.numeric函数将因子转化为数字
CASchools$HiSTR <- as.numeric(CASchools$size >= 20)

# 附加 HiEL 到 CASchools
CASchools$HiEL <- as.numeric(CASchools$english >= 10)

# 估计交互模型
bci_model <- lm(score ~ size + HiEL + size * HiEL, data = CASchools)

# 输出稳健的系数总结
coeftest(bci_model, vcov. = vcovHC, type = "HC1")
```

]

.panel[.panel-name[Output]

```
## 
## t test of coefficients:
## 
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 682.24584   11.86781 57.4871   <2e-16 ***
## size         -0.96846    0.58910 -1.6440   0.1009    
## HiEL          5.63914   19.51456  0.2890   0.7727    
## size:HiEL    -1.27661    0.96692 -1.3203   0.1875    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

]
]
.panel[.panel-name[注]
$$ \hat{TestScore}=682.4-0.97STR+5.6HiEL-1.28(STR\times HiEL)$$
- 低英语学习者百分率（ `$HiEL=0$` ）的学区，回归线估计为 `$$Y_i=682.2-0.97STR_i$$`

- 高英语学习者百分率（ `$HiEL=1$` ）的学区，回归线估计为 `$$Y_i=682.2+5.6-0.97STR_i-1.28STR_i=678.8-2.25STR_i$$`
]]
---

###在学生/教师比和英语学习者百分率中的应用
.panelset[
.panel[.panel-name[注]
- 因此
 - 在低英语学习者百分率学区内减少1个单位学生/教师比则预计测试成绩提高0.97分
 
 - 在高英语学习者百分率学区内减少1个单位学生/教师比则预计测试成绩提高2.25分
 
 - 两效应之差1.28分即为交互项系数

- 降低学生/教师比对测试成绩的效应取决于还在学习英语的学生百分率是高还是低吗？
]
.panel[.panel-name[]
.panel[.panel-name[Code]

```r
# 识别 英语学习者百分率PctEL >= 10的观测值
id <- CASchools$english >= 10

# 用红色点标识低英语学习者百分率（HiEL=0）的观测值
plot(CASchools$size[!id], CASchools$score[!id],
#lim设置坐标轴范围
     xlim = c(0, 27),
     ylim = c(600, 720),
     pch = 20,
     col = "red",
     main = "",
     xlab = "Class Size",
     ylab = "Test Score")

# 用绿色点标识高英语学习者百分率（HiEL=1）的观测值
points(CASchools$size[id], CASchools$score[id],
     pch = 20,
     col = "green")

# 读取交互模型的估计系数
coefs <- bci_model$coefficients

# 画出低英语学习者百分率（HiEL=0）的估计回归线
abline(coef = c(coefs[1], coefs[2]),
       col = "red",
       lwd = 1.5)

# 画出高英语学习者百分率（HiEL=1）的估计回归线
abline(coef = c(coefs[1] + coefs[3], coefs[2] + coefs[4]),
       col = "green", 
       lwd = 1.5 )

# 在图上添加标注
legend("topleft", 
       pch = c(20, 20), 
       col = c("red", "green"), 
       legend = c("HiEL = 0", "HiEL = 1"))
```

]

.panel[.panel-name[Output]

![](Lecture_7_Nonlinear_Regression_files/figure-html/unnamed-chunk-16-1.png)

]
]
]
---

###在学生/教师比和英语学习者百分率中的应用
- 前面讲的OLS回归可用于检验总体回归线的假设
 - 检验 `$HiEL$` 系数和交互项 `$STR \times HiEL$` 系数均为0的联合假设的 `$F$` 统计量 `$\longrightarrow$` 两直线相同的假设
 
     - `$F=89.9 \longrightarrow 1\%$` 水平下显著，拒绝原假设
 
 - 检验交互项 `$STR \times HiEL$` 系数为 
`$0\longrightarrow$` 两直线斜率相同的假设

- `$t=-\frac{1.28}{0.97} \approx -1.32,1.32<1.645 \longrightarrow 10\%$` 水平下不能拒绝
 
 - 检验 `$HiEL$` 系数为 `$0\longrightarrow$` 两直线截距相同的假设

- `$t=-\frac{5.6}{19.5} \approx 0.29 \longrightarrow 5\%$` 水平下不能拒绝
     
  - 检验 `$STR$` 系数和交互项 `$STR \times HiEL$` 系数均为0的联合假设的 `$F$` 统计量 `$\longrightarrow$` 不包含学生/教师比的假设
  
- 回归变量 `$HiEL$` 和 `$STR \times HiEL$` 高度相关，导致单个系数的标准误差较大
---

###两个连续变量的交互作用
- 现在我们考虑两个自变量都连续的情况
`$$Y_i=\beta_0+\beta1X_{1i}+\beta_2X_{2i}+\beta_3(X_{1i}\times X_{2i})+u_i$$`
- `$Y_i$` 表示第i个职工的收入对数， `$X_{1i}$` 表示工作经验， `$X_{2i}$` 表示受教育的年限

- 交互项使 `$X_1$` ( `$X_2$` )  的单位变化效应依赖于 `$X_2$` ( `$X_1$` )
 - 固定 `$X_2$` ， `$X_1$` 变化引起 `$Y$` 的变化
 `$$\frac{\Delta Y}{\Delta X_1}=\beta_1+\beta_3X_2$$`
 
 - 固定 `$X_1$` ， `$X_2$` 变化引起 `$Y$` 的变化
 `$$\frac{\Delta Y}{\Delta X_2}=\beta_2+\beta_3X_1$$`
 
 - `$\Delta Y=(\beta_1+\beta_3X_2)\Delta X_1+(\beta_2+\beta_3X_1)\Delta X_2+\beta_3 \Delta X_1 \Delta X_2$`
---

###小结
- 非线性回归函数

- 斜率依赖于一个或多个自变量的取值
- 多项式回归

- 三种对数回归模型
 - 线性对数模型
 
 - 对数线性模型
 
 - 双对数模型
- 三种交互作用与交互项
 - 二值变量与二值变量
 
 - 二值变量与连续变量
 
 - 连续变量与连续变量